16.Сопряженный оператор и его свойства. Матрица сопряженного оператора
Пусть A: V→V – линейный оператор, где V=U или V=E.
Определение:
Оператор ![]()
![]() Наз-ся сопряженным к оператору A, если
Наз-ся сопряженным к оператору A, если ![]() .
.
Теорема:
Каждый линейный оператор A имеет единственный сопряженный оператор ![]() . Оператор
. Оператор ![]() также является линейным.
также является линейным.
Доказательство:
(для V=U)
![]() скалярное произведение
скалярное произведение ![]() явл-ся полуторалинейной формой в унитарном пр-ве U следовательно по теореме о представлении полуторалинейной формы существует единственный линейный оператор
явл-ся полуторалинейной формой в унитарном пр-ве U следовательно по теореме о представлении полуторалинейной формы существует единственный линейный оператор ![]() такой, что
такой, что ![]() . По определению сопряж. Оператора
. По определению сопряж. Оператора ![]() #
#
Замечание: Аналогично теорема доказывыается и для V=E.
Свойства сопряженного оператора:
1. ![]() , здесь I – тождественный оператор. 2.
, здесь I – тождественный оператор. 2. ![]()
3. ![]() 4.
4. ![]() 5. Если существует
5. Если существует ![]() , то
, то ![]()
6. Если подпространство ![]() инвариантно относит. оператора A, то подпространство
инвариантно относит. оператора A, то подпространство ![]() инвариантно относит. сопряж. оператора
инвариантно относит. сопряж. оператора ![]() .
.
Доказательства свойств (V=U):
1) ![]() #
#
2) ![]() =
=
=![]() #
#
3) ![]() , отсюда из рав-ва операторов следует
, отсюда из рав-ва операторов следует ![]() #
#
4) ![]()
![]() следовательно
следовательно ![]()
5) ![]() если существует
если существует ![]() , то
, то ![]() .
.
![]() или
или ![]() , след-но
, след-но ![]() #
#
6) Существует ![]() , тогда
, тогда ![]() и
и ![]() , но
, но ![]() след-но
след-но
![]() #
#
Пусть ![]() – ОНБ в унитарн. пр-ве U:
– ОНБ в унитарн. пр-ве U: ![]() – матрица опер. A,
– матрица опер. A, ![]() – матр. сопряж. оператора
– матр. сопряж. оператора ![]() . Найдем связь между
. Найдем связь между ![]() и
и ![]() .
.
По определению матрицы лин. оператор ![]() , тогда запишем
, тогда запишем
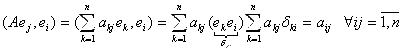 Итак,
Итак, ![]() , аналогично можно записать
, аналогично можно записать ![]() . Запишем
. Запишем
![]() , т. е.
, т. е. ![]() – матрица сопряж. опер.
– матрица сопряж. опер. ![]() .
.
| < Предыдущая | Следующая > |
|---|