14.Ортогональное дополнение подпространства унитарного и евклидова пространства. Теорема о представлении унитарного пространства в виде прямой суммы линейных подпространств

Определение:

Два подпространства и унитарного (евклидова) пространства наз-ся ортогональными , если : или

Лемма 1:

Если , то {θ}

Доказательство: Пусть , т. е. и , т. к. , то θ #

Пусть ─ подпространство пространства ( или ). #

Определение:

Ортогональным дополнением подпространства пространства наз-ся множество всех в-в, ортогональных подпространству , т. е. =

Пример:

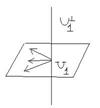
V-пространство всех геометрических (свободных) вр-в

-подпространство всех в-в параллельных некоторой плоскости

─ подпространство всех в-в, перпендикулярных данной плоскости.

Утверждение:

Ортогональное дополнение произвольного подпространства пространства V само является подпространством данного пространства

Доказательство: В самом деле, : #

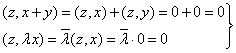
Лемма 2 (критерий):

Пусть ─ базис в подпространстве . Вектор ;

Доказательство:

Необходимость: Пусть , тогда в том числе .

Достаточность: Пусть , поскольку : , то #

Теорема:

Унитарное (евклидово) пространство есть прямая сумма произвольного подпространства и его ортогонального дополнения , т. е. (прямая сумма)

Доказательство:

Пусть ── ОНБ в подпространстве .

Возьмем произвольный в-р и сопоставим следующий в-р:

имеем (скалярное умножение на ):

Следовательно по Лемме 2

, т. е. : , где , . Но

Следовательно по Лемме 1

{θ}, откуда по определению прямой суммы вытекает, что #

Следствие 1:

Доказательство: Доказательство следует из Теоремы 2 § 5 гл. III #

< Предыдущая		Следующая >