05.Билинейные формы в линейном пространстве. Симметрические и кососимметрические билинейные формы

Пусть V – вещественное линейное пространство.

Определение: Билинейной формой называется числовая функция A(X,Y) 2-х векторных аргументов X и y (), линейная как по 1-му, так и по 2-ому аргументу, и удовлетворяющая следующим условиям:

1) A(X+Y,Z)=A(X,Z)+A(Y,Z)

2) A(X,Y+Z)=A(X,Y)+A(x, z)

3) A(λx,Y)= λA(X,Y)

4) A(X, λy)= λA(X,Y)

Пример 1:

Пусть F(X) и G(Y) - две линейные формы, т. е. линейные операторы, отображающие пространство V в числовое множество. Тогда A(X,Y)=F(X)G(Y) - билинейная форма.

Пример 2:

Скалярное производные 2-х векторов:

тогда можно записать так - билинейная форма.

Получим теперь выражение для билинейной формы в общем виде, пусть - базис в V и тогда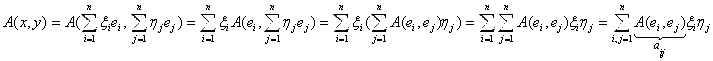

Определение: Матрица , где называется матрицей AE билинейной формы A(X,Y) в базисе . Элементы этой матрицы называются коэффициентами билинейной формы в данном базисе.

Определение: Билинейная форма A(X,Y) называется симметрической (кососимметрической), если .

Замечание 1: Всякая симметричная билинейная форма A(X,Y) однозначно определяется своими значениями для совпадающих аргументов. В самом деле:

Замечание 2: Если A(X,Y) - симметричная билинейная форма, то ее матрица AE также является симметричной в любом базисе. В самом деле,

Следствие. Представление называется общим видом билинейной формы A(X,Y) в N – мерном линейном пространстве.

< Предыдущая		Следующая >