04.Диагонализуемость линейного оператора

Определение: Квадратная матрица А порядка N называется диагональной, если она имеет вид:

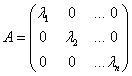
Определение: Линейный оператор называется диагонализуемым, если в линейном пространстве существует базис, в котором матрица А данного линейного оператора имеет диагональный вид.

Теорема 1: (критерий диагонализуемости матрицы линейного оператора).

Пусть - базис в линейном пространстве V. Матрица линейного оператора в этом базисе будет диагональна тогда и только тогда, когда базисные вектора являются собственными векторами А. Матрица в базисе из собственных векторов имеет следующий диагональный вид:

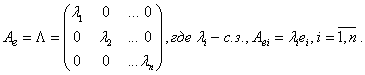
Доказательство:

Необходимость:

Пусть в базисе имеем . Тогда по определению матрицы линейного оператора можно записать:

Достаточность:

Пусть базис состоит из собственных векторов. Тогда .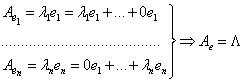

Теорема 2: (Достаточное условие диагонализуемости матрицы линейного оператора).

Пусть dimV=N, если линейный оператор имеет N попАрно различных с. з., , то в линейном пространстве V существует базис , в котором матрица AE оператора А имеет диагональный вид, причем этот базис состоит из с. в-в.

Доказательство: Пусть - собственные вектора, отвечающие попарно различным собственным значениям , тогда по Свойству 2 образуют базис (т. к. dimV=N) отсюда по Теореме 1 (критерию) матрица AE оператора А в этом базисе диагональна. #

Замечание 1: Обратная теорема неверна. В качестве примера можно рассмотреть тождественный оператор , при этом матрица AE этого оператора в базисе из собственных векторов имеет диагональный вид, однако с. з.-я совпадают, т. е. не являются попарно различными.

Следствие: Если все корни характеристического уравнения оператора А попарно различны, то существует невырожденная матрица такая, что матрица является диагональной.

Доказательство: Доказательство вытекает из формулы преобразования матрицы линейного оператора при переходе от базиса (Е) к базису (Е`), который состоит из с. векторов и значит матрица является диагональной.

< Предыдущая		Следующая >