03.Свойства собственных значений и собственных векторов линейного оператора

1) Пусть - собственные векторы линейного оператора А, отвечающие одному и тому же

С. з. – ю λ. Тогда их линейная комбинация также является с. в., отвечающим тому же с. з. – ю λ.

Доказательство:

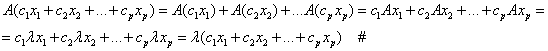
2) Если - различные с. зн-я. линейного оператора A, то отвечающие им собственные векторы л. н.з.

Доказательство: Будем доказывать методом математической индукции. Так как , то л. н.з., пусть утверждение справедливо для N векторов , т. е. - л. н.з. Присоединим к ним вектор и рассмотрим равенство (*).

Подействуем оператором A На (*). Получим или . Вычтем из последнего равенства равенство (*), умноженное на :.

Т. к. - попарно различны и - л. н.з., то . Тогда из (*) получаем, что #

Определение: Квадратная матрица А порядка N называется диагональной, если она имеет вид:

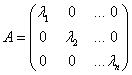
Определение: Линейный оператор называется диагонализуемым, если в линейном пространстве существует базис, в котором матрица А данного линейного оператора имеет диагональный вид.

< Предыдущая		Следующая >