02.Собственные значения и собственные векторы линейного оператора А

Собственные значения и собственные векторы линейного оператора А.

Пусть , где V – n - мерное линейное пространство.

Определение: Число λ - называется собственным значением (с. з.) линейного оператора А, если такой, что . При этом элемент (вектор) X называется собственным вектором (с. в.) оператора А.

Здесь , если V – вещественное линейное пространство, и , если V – комплексное линейное пространство.

Критерий (существования собственного значения линейного оператора А):

Для того, чтобы λ было собственным значением линейного оператора А, необходимо и достаточно чтобы это число было корнем характеристического уравнения оператора А.

Доказательство:

Пусть - произвольный базис пространства V. - матрица оператора А в данном базисе. Тогда имеем в обе стороны (необходимость и достаточность):

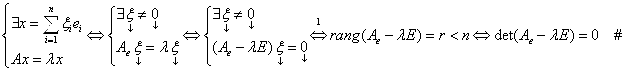
(1по критерию существования ненулевых решений однородной СЛАУ.)

Правила нахождения с. з. и с. в. линейного оператора А.

1) Выбираем в пространстве базис и записываем матрицу оператора .

2) Находим все собственные значения как корни характеристического уравнения .

3) Решая однородную СЛАУ для каждого с. з.- я находим координаты соответствующих ему собственных векторов.

Определение: Множество всех собственных значений оператора А называется спектром оператора А.

< Предыдущая		Следующая >