3.07.3. Следствия из формулы Эйлера

1. Число граней любой плоской укладки планарного -графа постоянно и равно .

Отметим также, что число граней , где – циклический ранг графа .

2. Пусть выпуклый многогранник имеет В вершин, Р Ребер и Г граней. Тогда .

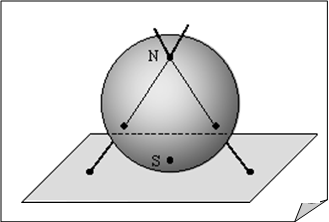
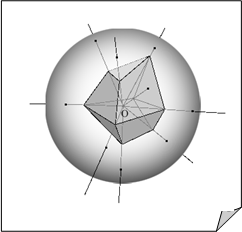Доказательство. Поместим многогранник внутрь сферы. Выберем некоторую внутреннюю точку O многогранника и проведем через нее всевозможные лучи, отображая точки поверхности многогранника в точки сферы (см. рис.). Получим укладку поверхности многогранника на сфере, представляющую собой некоторый граф на сфере. Выберем некоторую внутреннюю точку одной из граней графа на сфере и проведем через диаметрально противоположную точку касательную плоскость к сфере. Проведя через всевозможные лучи, отобразим сферу на плоскость (точка перейдет в бесконечно удаленную точку плоскости). При этом граф со сферы отобразится в некоторый плоский граф на плоскости . Заметим, что при этом грань, содержащая точку , отобразится во внешнюю грань графа на плоскости . Композиция обоих отображений, очевидно, определяет биекцию между множествами вершин, ребер, граней данного многогранника и такими же множествами полученного плоского графа. Поэтому полученный граф имеет В вершин, Р Ребер и Г граней. Остается воспользоваться формулой Эйлера для графов.

3. Для всякого планарного -графа порядка .

Доказательство. Пусть – плоский связный -граф с гранями. Всякая грань ограничена не менее, чем 3 ребрами. Всякое ребро либо разграничивает 2 грани, либо ни одной (если не принадлежит ни одному циклу). Поэтому . По формуле Эйлера . Поэтому , откуда и получаем нужное неравенство.

4. Граф не является планарным.

Доказательство. Действительно порядок полного графа равен 5, а число его ребер . Если бы этот граф был планарным, то для него выполнялось бы следствие 3, т. е. , которое не верно. Следовательно, K5 -- не планарный.

5. Граф не является планарным.

Доказательство. Данный граф имеет вершин и ребер. Предположим, что он планарный. Тогда он имеет граней. В то же время, всякая грань двудольного графа ограничена четным числом ребер (все циклы имеют четную длину), т. е. не менее, чем четырьмя ребрами. Поэтому . Но для это неравенство приводит к , что не верно. Значит, предположение о планарности графа ошибочно.

6. В любом простом планарном графе существует вершина степени не более 5.

Доказательство. Без потери общности можно считать, что данный граф – связный планарный -граф порядка . Тогда согласно следствию 3 имеем: . Предположим противное, что степени всех вершин графа не менее 6. Тогда по лемме о рукопожатиях , т. е. , что противоречит неравенству в следствии 3. Утверждение доказано.

< Предыдущая		Следующая >