3.07.4. Гомеоморфные графы. Критерий планарности
Рассмотрим две новые операции на графах.
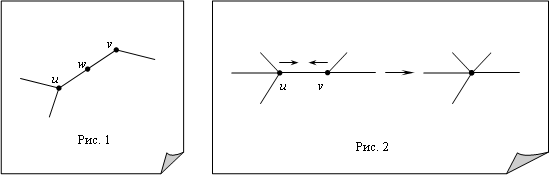 Подразбиением ребра
Подразбиением ребра ![]() графа
графа ![]() называется операция удаления ребра
называется операция удаления ребра ![]() с добавлением новой вершины
с добавлением новой вершины ![]() и двух ребер
и двух ребер ![]() и
и ![]() . На рисунке графа
. На рисунке графа ![]() это означает, что добавляется новая вершина
это означает, что добавляется новая вершина ![]() на ребре
на ребре ![]() , которое, таким образом, разбивается на два ребра (рис. 1).
, которое, таким образом, разбивается на два ребра (рис. 1).
Стягивание смежных вершин ![]() и
и ![]() графа
графа ![]() означает удаление ребра
означает удаление ребра ![]() и замена двух вершин
и замена двух вершин ![]() И
И ![]() одной вершиной, которая соединяется ребрами со всеми вершинами графа
одной вершиной, которая соединяется ребрами со всеми вершинами графа ![]() , с которыми были смежны вершины
, с которыми были смежны вершины ![]() и
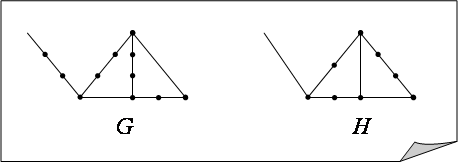
и ![]() (рис. 2).
(рис. 2).
 |
Графы
Гомеоморфными являются, в частности, любые две простые цепи, любые два простых цикла.
Теорема (Понтрягин – Куратовский). Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных ![]() или
или ![]() .
.
Теорема (Вагнер). Граф планарен тогда и только тогда, когда в нем нет подграфов, стягиваемых к графам ![]() или
или ![]() .
.
Отметим в заключение, что стягивая любое ребро планарного графа, вновь получим планарный граф. Если же дан непланарный граф, то стянув одно или несколько ребер можно получить планарный граф.
| < Предыдущая | Следующая > |
|---|