3.07.2. Планарные графы. Формула Эйлера

Граф называется Планарным, если он может быть уложен на плоскости. Непосредственная укладка планарного графа, т. е. его рисунок, на котором ребра не пересекаются, называется Плоским Графом.

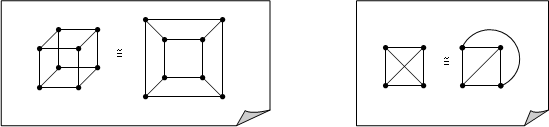Например, трехмерный куб является планарным графом (см. рис.), полный граф также планарный.

Ребра плоского графа, образующие простые циклы, разбивают плоскость на несколько частей, которые называются Гранями плоского графа. Так, граф куба (см. рис.) имеет 6 граней (5 внутренних и одну внешнюю), граф имеет 4 грани (3 внутренних и 1 внешнюю). Внешнюю грань имеет всякий планарный граф, даже если в нем нет циклов.

Плоский граф вмести со всеми своими вершинами, ребрами, а также гранями называют Плоской картой.

Теорема. Для всякого связного плоского -графа с F гранями справедливо равенство (формула Эйлера) : .

Доказательство. Пусть – остов графа . T имеет только одну (внешнюю) грань и ребро, т. е. в этом случае: , и очевидно формула справедлива. Будем поочередно добавлять к остову недостающие ребра графа . При этом число вершин N не меняется, число ребер увеличивается на 1. Число граней также увеличивается на 1. Действительно, если добавленное ребро соединяет две вершины, принадлежащие какому-либо циклу, то грань, ограниченная данным циклом, разбивается на две грани. В противном случае, новая внутренняя грань появляется за счет части внешней грани. В любом случае число граней увеличивается на 1. Таким образом, после добавления каждого ребра формула остается верной. Значит, когда будут восстановлены все ребра и получен граф , формула также окажется верной.

< Предыдущая		Следующая >