3.02.1. Основные числовые характеристики и матрицы графа. Степени вершин графа
Степенью вершины V графа G называется число инцидентных ей рёбер, т. е. число рёбер, выходящих из данной вершины. (В случае псевдографов каждая петля добавляет 2 в степень вершины). Обозначается степень вершины V графа G: degGv или просто deg V, если ясно, о каком графе G идет речь.
Вершина степени 0 называется Изолированной. Вершина степени 1 называется Концевой (или Висячей). Ребро, инцидентное концевой вершине также
 Называется Концевым.
Называется Концевым.
Вершина V Графа G, смежная со всеми другими вершинами G, называется Доминирующей. Её степень degGv очевидно равна |G| --1.
Граф G называется Регулярным (или, по-другому, Однородным), если степени всех его вершин равны. Эта общая степень всех вершин регулярного графа G называется степенью регулярного графа G и обозначается deg G.
Последовательность степеней вершин графа G, записанная в каком либо порядке называется степенной последовательностью графа G. Например, граф на рисунке справа имеет степенную последовательность (3, 3, 1, 0, 1, 2).
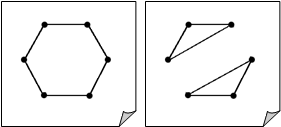 Понятно, что изоморфные графы имеют одинаковые (с точностью до порядка следования элементов) степенные последовательности. Однако, из этого совпадения степенных последовательностей двух графов ещё не следует их изоморфность. На следующих двух рисунках изображены два неизоморфных регулярных графа степени 2.
Понятно, что изоморфные графы имеют одинаковые (с точностью до порядка следования элементов) степенные последовательности. Однако, из этого совпадения степенных последовательностей двух графов ещё не следует их изоморфность. На следующих двух рисунках изображены два неизоморфных регулярных графа степени 2.
Таким образом, степенная последовательность не определяет граф полностью и не может
|
Степенная последовательность не может быть произвольным набором чисел, а обладает определёнными свойствами.
Лемма 1 ("о рукопожатиях"). Сумма степеней всех вершин графа G есть число чётное, ровно в два раза большее числа рёбер графа G, т. е.
Доказательство: Действительно, подсчитаем количество рёбер графа G, просматривая поочередно все вершины графа G и считая рёбра выходящие из этих вершин. Так как из каждой вершины V выходит degGV рёбер, то мы получим сумму:
Но при этом каждое ребро будет учтено 2 раза: один раз, когда рассматривался один его конец, другой раз, когда -- второй. Таким образом, лемма верна.
Из леммы 1 вытекает
Следствие. В любом графе число вершин нечётной степени является чётным.
Доказательство. В самом деле, иначе, если бы сумма целых чисел содержала нечётное число нечетных слагаемых, то она, очевидно, была бы нечётной, что противоречит лемме о рукопожатиях.
В ориентированных графах для каждой вершины V дополнительно рассматривается также полустепень исхода и полустепень захода. Полустепенью исхода вершины V называется число дуг графа G, для которых V Является началом, а Полустепенью захода – число дуг, для которых V является концом. Обозначаются полустепени захода и исхода графа G соответственно deg-V и deg+V. При этом полная степень degV = deg-V+ deg+V. Поскольку каждая дуга имеет ровно одно начало и один конец, то справедлива
Лемма 2. Сумма полустепеней исхода всех вершин графа G Равна сумме полустепеней захода, т. е.
| < Предыдущая | Следующая > |
|---|