3.01.5. Количество различных графов порядка n

Лемма 1. Число помеченных графов порядка N равно 2N(N - 1) / 2.

Доказательство. Действительно, существует N(N-1)/2 пар вершин, для каждой из которых имеется ровно 2 возможности: данная пара вершин соединена ребром или нет. Поэтому, когда вершины помечены, то можно построить ровно 2N(N-1)/2 различных (с учетом пометки) графов.

Для числа абстрактных (непомеченных) графов порядка N точной формулы не существует. Однако, известно, что оно асимптотически стремится к величине 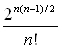. Это означает, что при N® предел отношения точного числа неизоморфных простых графов к указанной величине равен 1.

Этот факт представляется достаточно ясным, поскольку N непомеченных вершин графа можно пометить N! способами (количество пометок, очевидно, совпадает с числом перестановок из N элементов). Поэтому следует ожидать, что каждый непомеченный граф даст N! неизоморфных помеченных. Однако, это не всегда так. Например, все пометки пустого (а так же полного) графа приводят к одному и тому же помеченному графу. Никакие другие пометки графа на последнем рисунке не дадут новых помеченных графов. По этой причине в последнем случае из данного непомеченного получаем не 3! = 6, а только 3 помеченных графа. Таким образом, в случае непомеченных графов указанная величина представляет собой, не точную формулу, а лишь оценку.

< Предыдущая		Следующая >