3.01.4. Изоморфные графы

Одной из особенностей графов является то, что при их изображении на плоскости совершенно не важно, как расположены вершины друг относительно друга. Поэтому одному и тому графу могут соответствовать различные его изображения. Кроме того, именно такие рисунки, представляющие собой простейший способ задания графа, зачастую и называют графами. Чтобы отличать рисунки, отвечающие одному и тому же графу, от рисунков, изображающих различные графы, введем следующее понятие.

Определение. Два графа G и H называются Изоморфными, если существует биекция F: V(G) ® V(H), сохраняющая смежность, т. е. такое биективное отображение, при котором образы вершин V и U графа G смежны в H тогда и только тогда, когда U и V смежны в графе G. Отображение F, обладающее указанным свойством, называется Изоморфизмом.

Если графы G и H изоморфны, то пишут G @ H.

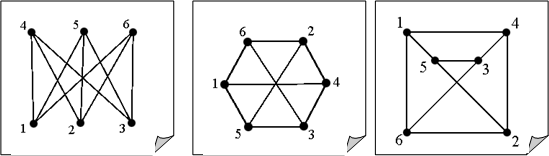Например, все три графа на следующих рисунках изоморфны друг другу (изоморфизм определяется нумерацией вершин)

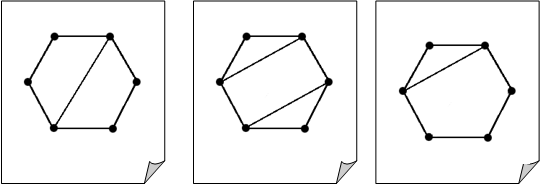
А на следующих трех рисунках представлены попарно неизоморфные графы.

Очевидно, что отношение изоморфности на множестве графов является отношением эквивалентности (оно рефлексивно, симметрично и транзитивно). Следовательно, множество всех графов разбивается на классы изоморфных графов так, что разные классы не пересекаются. Все графы, попадающие в один класс естественно отождествлять, т. е. считать совпадающими (они могут отличаться лишь рисунком или природой своих элементов). В тех случаях, когда нужно подчеркнуть, что рассматриваемые графы отличаются лишь с точностью до изоморфизма, принято говорить об "Абстрактных графах". По сути дела, абстрактный граф -- это класс изоморфных графов.

В некоторых ситуациях все же приходится различать изоморфные графы и тогда возникает понятие "Помеченный граф". Граф порядка N называется помеченным, если его вершинам присвоены метки, например, номера 1, 2, 3, …, N. В этом случае вершины графа G отождествляют с их номерами, т. е. полагают, что V(G) = {1, 2, 3, …, N}. Помеченные графы G и H считаются совпадающими (изоморфными) при дополнительном условии, что E(G) = E(H).

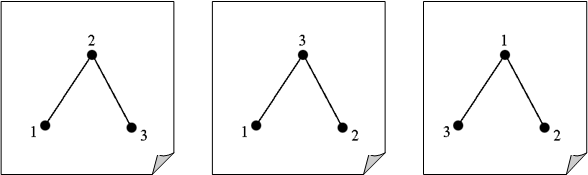
На следующих рисунках изображены три попарно неизоморфные помеченные графы (которые, очевидно, совпадают друг с другом, если убрать пометки).

Для мульти-, псевдо - и ориентированных графов понятие изоморфности определяется аналогично, как биективность, при которой помимо смежности вершин и ребер сохраняются также кратность ребер, петли и направления дуг.

< Предыдущая		Следующая >