3.02.2. Матрица смежности
Пусть G – помеченный граф порядка N , V(G) = {1, 2, 3, …, N}. Матрицей смежности графа G называется бинарная N´N-матрица M(G) = (Mij), такая, что Mij = 1, если вершина I смежна с вершиной J, и Mij = 0, в противном случае.
Легко видеть, что матрица смежности простого графа G является симметричной, с нулями на главной диагонали. Число единиц в каждой строке (каждом столбце) равно степени соответствующей вершины. Понятно, что и обратно, всякой бинарной матрице с указанными свойствами соответствует некоторый простой граф. Таким образом, матрица смежности является одним из способов задания графов.
Для мульти - и псевдографов матрица смежности определяется так, что:
Mij = ![]()
Для ориентированного графа G:
Mij = ![]()
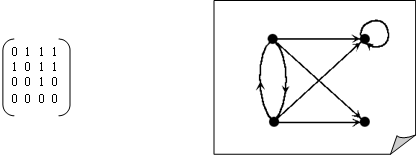 Таким образом, всякая бинарная матрица является матрицей смежности соответствующего ориентированного графа. Например, следующей матрице соответствует изображенный далее граф.
Таким образом, всякая бинарная матрица является матрицей смежности соответствующего ориентированного графа. Например, следующей матрице соответствует изображенный далее граф.
Абстрактный граф приводит к различным матрицам смежности в зависимости от нумерации вершин.
Теорема. Графы изоморфны тогда и только тогда, когда их матрицы смежности получаются друг из друга путём парных перестановок одинаковых строк и столбцов.
Доказательство. Действительно таким перестановкам (переставляются одновременно, как одна операция, две строчки и два столбца с одинаковыми номерами) соответствует перенумерация вершин графа, что очевидно приводит к изоморфному графу.
Из теоремы, в частности, следует, что ранги матриц смежности изоморфных графов совпадают. Этот общий ранг различных матриц смежности изоморфных графов называется рангом соответствующего абстрактного графа G и обозначается rg G. Совпадают так же характеристические многочлены и собственные значения матриц смежности изоморфных графов, которые называются, соответственно, характеристическим многочленом и спектром графа G.
Для двудольного графа G, с долями V1 = {X1, X2, …, Xn} и V2 = {Y1, Y2, …, Ym} рассматривается так же приведённая N´M-матрица смежности, такая, что Mij = 1, если вершина Xi смежная с Yj, и Mij = 0 в противном случае.
Для взвешенных графов вместо матрицы смежности обычно рассматривается матрица весов, элементы которой mij = вес рёбра {i, j}. Отсутствующим рёбрам присваивается вес ∞ или 0, в зависимости от решаемой задачи.
| < Предыдущая | Следующая > |
|---|