2.3.3. Теоремы о функциональной полноте
Одна из сфер применения булевых функций -- синтез логических схем; при этом булевым функциям соответствуют определённые функциональные элементы (детали). Полнота системы функций означает, что, пользуясь только элементами соответствующих этим функциям типов, можно собрать любую логическую схему. При схемной реализации константы 0 и 1 специальных элементов не требуют. Поэтому существует ослабленное понятие функциональной полноты.
Определение. Система функций S называется полной в слабом смысле, если система ![]() является полной (в сильном смысле, т. е. в смысле определения в пункте 1).
является полной (в сильном смысле, т. е. в смысле определения в пункте 1).
Теорема 1. (Пост). Для того, чтобы система функций S была полной в слабом смысле необходимо и достаточно, чтобы она содержала хотя бы одну нелинейную функцию и хотя бы одну немонотонную функцию.
Теорема 2. (Пост). Для того, чтобы система функций была полной (в сильном смысле) необходимо и достаточно, чтобы она не содержалась целиком ни в одном из замкнутых классов K0, K1, KS, KM и KL.
Схема доказательства. Необходимость очевидна, поскольку никакой из перечисленных классов не совпадает целиком с множеством всех булевых функций.
Достаточность доказывается в 3 этапа:
1) построение констант 0 и 1 с помощью функций ![]() ,
, ![]() и
и ![]() ;
;
2) построение функции–отрицания с помощью констант 0, 1 и функции ![]() ;
;
3) построение конъюнкции с помощью констант 0, 1, функции ![]() и
и ![]() .
.
После этого учитывая, что дизъюнкция представляется через конъюнкцию и отрицание ![]() и что система
и что система ![]() полная, достаточность доказана.
полная, достаточность доказана.
Замечание. Из теоремы, в частности, следует, что всякий замкнутый класс, отличный от множества всех булевых функций, содержится в одном из классов K0, K1, KS, KM, KL. По этой причине перечисленные классы называют Основными замкнутыми классами пространства булевых функций.
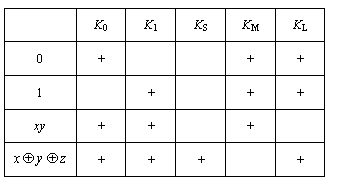 Пример. Рассмотрим совокупность булевых функций
Пример. Рассмотрим совокупность булевых функций ![]() . Составим и заполним следующую таблицу, отмечая знаком «+» функции, принадлежащие соответствующим классам. Заполнение первых трех строчек очевидно. Кроме того, непосредственно видно, что функция
. Составим и заполним следующую таблицу, отмечая знаком «+» функции, принадлежащие соответствующим классам. Заполнение первых трех строчек очевидно. Кроме того, непосредственно видно, что функция ![]() сохраняет константы 0 и 1. Уже по форме записи она является линейной. Самодвойственоость функции
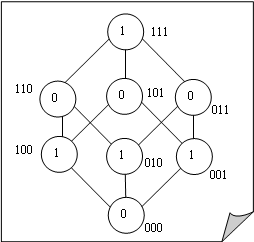
сохраняет константы 0 и 1. Уже по форме записи она является линейной. Самодвойственоость функции ![]() вытекает из таблицы значений (см. на следующей странице), а монотонность очевидна из диаграммы Хассе.
вытекает из таблицы значений (см. на следующей странице), а монотонность очевидна из диаграммы Хассе.
Из таблицы видно, что множество функций S не содержится полностью ни в одном из пяти основных замкнутых классов (нет ни одного столбца целиком заполненного символами «+»). Следовательно, система функций S является полной (в сильном смысле), а совокупность ![]() -- полная в слабом смысле.
-- полная в слабом смысле.
|
X |
Y |
Z |
|
|
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
| < Предыдущая | Следующая > |
|---|
 (
(