2.3.4. Базисы пространства булевых функций

Определение. Полная система функций называется Базисом пространства булевых функций, если любое собственное подмножество данной системы функций уже не является полным.

Другими словами, базис – это минимальная (но не по количеству, а в смысле отношения включения) полная система булевых функций.

Примеры. Система функций -- полная, но не базис, так как полными являются ее подмножества и (последнее вытекает из равенств и ). Множества и уже являются базисами. Они носят названия конъюнктивного и дизъюнктивного базиса Буля, соответственно. Нетрудно показать, что базисом является также множество -- базис Жегалкина.

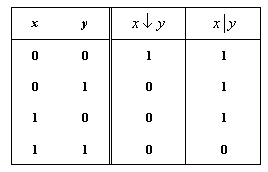подпись: x y

0 0 1 1
0 1 0 1
1 0 0 1
1 1 0 0 Рассмотрим две новые функции: (стрелка Пирса) и (штрих Шеффера), которые определяются таблицей значений, приведенной справа. Легко видеть также, что справедливы следующие представления этих функций:

==;

==.

Несложно проверить, что каждая из этих функций не принадлежит ни одному из основных замкнутых классов K0, K1, KS, KM, KL. Таким образом, одноэлементные множества {} и {} также являются базисами (базис Пирса и базис Шеффера).

Теорема. Всякий базис пространства булевых функций содержит не более четырёх функций.

Доказательство. Очевидно, что в базисе не более 5 функций – по одной функции для каждого из пяти основных замкнутых классов (не принадлежащей данному классу). Если какая-то функция в базисе не принадлежит сразу нескольким классам, то в базисе меньше пяти функций. Четырёх функций для базиса достаточно по следующей причине. В базисе обязательно имеется функция F(X1, X2, …, Xn), не сохраняющая константу 0, т. е. такая, что F(0, 0, …, 0) = 1. Существует две возможности: либо F(1, 1, … , 1) = 0, т. е. F(X1, X2,…, Xn) не сохраняет также константу 1; либо F(1, 1, … , 1) = 1 и тогда эта функция не может быть самодвойственной (для неё ). В любом случае этой функции достаточно на 2 класса.

Замечание. Оценку 4 (количества функций в базисе) в общем случае нельзя уменьшить, так как существуют базисы из четырёх функций, например, (см. пункт 3). Рассмотренные выше примеры показывают, что существуют также базисы, состоящие из одной, двух и трёх функций.

Пример. Рассмотрим функций S =. Покажем, что она является полной, и найдем все базисы, которые можно составить из функций данной совокупности. Для этого заполним следующую таблицу (впрочем, полнота S Следует уже из того, что S Содержит конъюнктивный базис Буля: ).

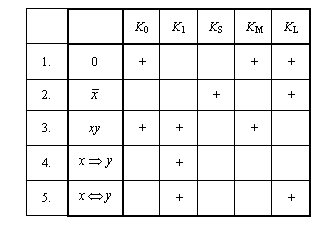подпись: k0 k1 ks km kl
1. 0 + + +
2.
+ +
3. xy + + +
4.
+
5.
+ + Чтобы найти все базисы, пронумеруем функции и отождествляя их с номерами запишем условие полноты в виде конъюнктивной формы. Для того, чтобы система функций была полной, необходимо и достаточно, чтобы для каждого из пяти основных замкнутых классов нашлась функция, которая данному классу не принадлежит (теорема Поста). Для класса K0 (см. таблицу) это может быть функция 2, 4 или 5; для класса K1 – 1 или 2 и т. д.. В результате получим:

Преобразуем полученную конъюнктивную форму в дизъюнктивную. В процессе преобразования будем формулу упрощать, пользуясь законами:

, .

Применив первый закон, сразу получим:

Далее, раскрывая скобки и упрощая согласно второму закону, окончательно получим:

Дальше дизъюнктивная форма не упрощается. Это означает, что имеется четыре базиса: 1) {1, 3, 5}; 2) {2, 3}; 3) {2, 4}; 4) {1, 4} (здесь цифры – номера функций).

Замечание. Метод, состоящий в записи конъюнктивной формы и её преобразовании в дизъюнкцию, который выше применялся для нахождения всех базисов данной совокупности функций, носит название Метода Петрика.

< Предыдущая		Следующая >