2.3.2. Основные замкнутые классы
А). Обозначим через К0 множество булевых функций F(X1, X2, …, Xn), сохраняющих константу 0, т. е. таких, что F(0, 0, … , 0) = 0.
Такими функциями являются, например, сама константа 0, конъюнкция Х1Х2, дизъюнкция ![]() , сумма по модулю два
, сумма по модулю два ![]() и др..
и др..
Не принадлежат классу К0 функции 1, ![]() ,
, ![]() ,
, ![]() и т. д.
и т. д.
Предложение. Класс функций К0 является замкнутым.
Доказательство. Действительно, пусть функция ![]()
![]() -- является композицией функций F0, F1, … , Fs. Тогда
-- является композицией функций F0, F1, … , Fs. Тогда ![]() , что и требовалось доказать.
, что и требовалось доказать.
Б). Пусть К1 – класс функций F(X1, X2, …, Xn), сохраняющих константу 1, т. е. таких, что F(1, 1, …, 1) = 1.
Например, константу 1 сохраняют функции 1, Х1Х2, ![]() , Х,
, Х, ![]() и другие. Не сохраняют константу 1 функции
и другие. Не сохраняют константу 1 функции ![]() ,
, ![]() и т. д..
и т. д..
Предложение. Класс функций К1 является замкнутым.
Доказательство такое же, как и для класса К0.
В). Пусть KS – класс Самодвойственных функций F(X1, X2, …, Xn), т. е. таких, что ![]() .
.
Примеры.
Очевидно, функции ![]() и
и ![]() являются самодвойственными. Рассмотрим также
являются самодвойственными. Рассмотрим также ![]() . Тогда
. Тогда ![]()
![]() -- самодвойственная.
-- самодвойственная.
В общем случае, самодвойственность функции легко проверять по таблице истинности: если столбец значений, после замены нулей на единицы, единиц на нули и переворачивания, не меняется, то функция – самодвойственная (см. пример в 3).
Предложение. Класс KS является замкнутым.
Доказательство. Пусть функция ![]() является композицией самодвойственных функций F0, F1, …, FS. Применяя принцип двойствен-ности, находим
является композицией самодвойственных функций F0, F1, …, FS. Применяя принцип двойствен-ности, находим
![]() ,
,
Что и требовалось доказать.
Г). Многочлены Жегалкина первой степени, т. е. функции вида ![]() , где
, где ![]()
![]() , называются Линейными функциями. В действительности, линейная функция представляет собой сумму нескольких различных переменных и, возможно, константы
, называются Линейными функциями. В действительности, линейная функция представляет собой сумму нескольких различных переменных и, возможно, константы
Понятно, что если вместо какой-либо переменной, или переменных подставить линейную функцию, то в результате (после возможных упрощений) снова получится линейная функция, и значит, справедливо
Предложение. Класс KL – линейных функций является замкнутым.
Д). Введём на множестве (Z2)n следующее отношение частичного порядка (свойства рефлексивности, антисимметричности и транзитивности легко проверяются). Если ![]() и
и ![]() -- два упорядоченных бинарных набора, то положим
-- два упорядоченных бинарных набора, то положим ![]() , если
, если ![]()
![]() . Если
. Если ![]() и
и ![]() , то ( как это и принято для отношения частичного порядка) будем писать:
, то ( как это и принято для отношения частичного порядка) будем писать: ![]() <
<![]() .
.
Например, (1,0,1,0) < (1,0,1,1); (0,0,1,0) < (1,0,1,0); (1,0,1,0) ù< (1,1,0,1).
Определение. Булева функция F(X1, X2, …, Xn) называется монотонной, если для любых бинарных наборов ![]() и
и ![]() таких, что
таких, что ![]() <
<![]() выполняется
выполняется ![]() .
.
Монотонными являются, например функции 0, 1, Xy, ![]() . В общем случае, монотонность, функции легко проверить по диаграмме Хассе данного отношения, которая представляет собой N-мерный куб. В вершинах куба запишем соответствующие значения функции. Если найдётся хотя бы одно ребро, в верхней вершине которого записан 0 а в нижней 1, то функция – не монотонная; в противном случае, если, поднимаясь по рёбрам, значение функции не уменьшается, то она – монотонная. Ниже приведены примеры немонотонной функции F(X, Y) (ребро, на котором не выполняется условие монотонности, выделено) и монотонной функции G(X, Y, Z).
. В общем случае, монотонность, функции легко проверить по диаграмме Хассе данного отношения, которая представляет собой N-мерный куб. В вершинах куба запишем соответствующие значения функции. Если найдётся хотя бы одно ребро, в верхней вершине которого записан 0 а в нижней 1, то функция – не монотонная; в противном случае, если, поднимаясь по рёбрам, значение функции не уменьшается, то она – монотонная. Ниже приведены примеры немонотонной функции F(X, Y) (ребро, на котором не выполняется условие монотонности, выделено) и монотонной функции G(X, Y, Z).
 |
|
X |
Y |
F(X, y) |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
|
|
|
|
 |
|
X |
Y |
Z |
G(X,Y,Z) |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
Предложение. Класс KM – монотонных функций является замкнутым.
Доказательство. Пусть функция F(…) = F0(F1(…), F2(…), …, FS(…)) является композицией монотонных функций. Если увеличить (в смысле введённого отношения частичного порядка) аргументы функции f(…), то увеличатся аргументы функций F1(…), F2(…), …, FS(…). Значения этих функций в силу их монотонности также увеличатся или не изменятся. Эти значения служат аргументами внешней функции F0(…), которая, будучи монотонной, также не уменьшится. Таким образом, F(…) обладает свойством монотонности, что и требовалось доказать.
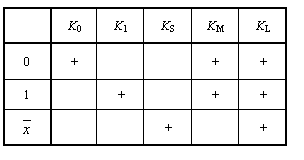 Замечание. Классы K0, K1, KS, KM и KL не являются полными (для каждого класса можно указать булеву функцию, которая ему не принадлежит). Все перечисленные пять замкнутых классов различны. Это видно, например, из следующей таблицы, в которой знак “ + “ означает, что соответствующая функция принадлежит данному классу (отсутствие знака – не принадлежит). Если бы какие-то два класса совпадали, то конечно расстановки знаков в соответствующих данным функциям строчках также совпадали бы.
Замечание. Классы K0, K1, KS, KM и KL не являются полными (для каждого класса можно указать булеву функцию, которая ему не принадлежит). Все перечисленные пять замкнутых классов различны. Это видно, например, из следующей таблицы, в которой знак “ + “ означает, что соответствующая функция принадлежит данному классу (отсутствие знака – не принадлежит). Если бы какие-то два класса совпадали, то конечно расстановки знаков в соответствующих данным функциям строчках также совпадали бы.
| < Предыдущая | Следующая > |
|---|