1.5.1. Понятие об алгебраических структурах

В математике и различных её приложениях важную роль играют такие математические объекты, которые называются алгебраическими структурами. Изучением их свойств занимается целый большой раздел математики – Высшая алгебра.

В широком смысле под алгебраической структурой понимают всякое множество, на котором заданы некоторые операции (т. е. законы, ставящие в соответствие одному или паре элементов по определённому правилу другой элемент), обладающие определёнными свойствами.

Примеры таких структур постоянно возникают в различных разделах математики. Это прежде всего:

1) Различные числовые множества с обычными операциями +, · на них.

2) Векторы с операциями [ · , · ], +, умножение на число.

3) Матрицы с операциями +, · , умножение на число.

4) Булева алгебра множеств с операциями , дополнение.

5) Множество функций (отображений) из R В R c операциями +, · , композиция.

6) Решётки (наличие sup и inf определяет наличие двух операций: (A,B) ® sup(A,B) и (A,B) ® inf(A,B) ).

Большинство свойств и результатов об этих множествах мы получаем, в основном опираясь на конкретную природу элементов этих множеств и на конкретный смысл операций над ними. В то же время многие результаты можно получить независимо от природы этих множеств и конкретного смысла операций, а исходя только из свойств этих операций.

Среди таких свойств таких операций рассматриваются: ассоциативность, коммутативность, дистрибутивность, наличие специальных элементов, обладающих определёнными свойствами (нулевой, единичный (нейтральный), обратный элемент к данному и т. д.).

В зависимости от количества операций и свойств, которыми они обладают, различают следующие алгебраические структуры.

1. Полугруппой Называется множество G, на котором задана бинарная операция * (часто её называют умножением и обозначают · ), для которой выполняется свойство ассоциативности, т. е.

" a, b,c Î G (A*B) *C = a*(B*C)

Примеры.

1. Множество отображений f : A®A с операцией произведение.

2. Множество отношений R A2 с операцией произведение отношений.

Если в полугруппе имеется нейтральный элемент Е (нулевой, единичный), т. е. такой, что A*E=e*A=a "AÎG, то полугруппа G называется Унитарной (полугруппой с нулём; полугруппой с единицей).

Если в полугруппе выполняется коммутативный закон, т. е. если "A,BÎG a*B = b*A, то полугруппа называется Коммутативной (или Абелевой).

Унитарная полугруппа называется Группой, если "АÎG существует обратный элемент B G, т. е. такой, что A*B = b*A = e.

Таким образом, в группе G Должны выполняться три свойства:

1. Ассоциативность.

2. Существование нейтрального элемента.

3. Существование обратного элемента для любого элемента из G.

Если дополнительно выполняется свойство коммутативности, то группа называется Коммутативной (или Абелевой), и в этом случае обычно применяется аддитивная символика, т. е. операция обозначается +, нейтральный элемент 0, обратный элемент к A Называют противоположным и обозначается: -а.

Примеры.

1) Множество натуральных чисел N -- унитарная абелевая полугруппа относительно обычной операции умножения чисел. В то же время N - абелевая полугруппа относительно сложения +.

2) Множество целых чисел Z -- абелевая группа относительно +.

3) Q \{0} -- абелевая группа относительно операции умножения чисел.

4) Sn – множество подстановок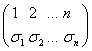На N Элементах с операцией произведение подстановок -- группа, но не абелева. Эта группа называется симметрической группой степени N.

Множество элементов конечной группы называется ее порядком. Из подсчета количества различных подстановок следует, что порядок симметрической группы ½Sn½= n!

5) Пусть G – множество движений квадрата переводящих его в себя (к которым относятся повороты, симметрии и их композиции). Нетрудно проверить, что G -- группа относительно операции композиции отображений, ее порядок ½G ½= 6 и вообще G = { e, J1, J2, J3, s1, s2, s3, s4}, где E --- тождественное отображение; J1, J2, J3 -- повороты в выбранном направлении (например, против часовой стрелки) на 90°, 180° и 270°; S1, s2, s3, s4 --- симметрии относительно диагоналей и средних линий. Легко видеть также, что в данной группе выполняются соотношения: JI4 = e, si2 = e и все произведения поворотов и симметрий являются перечисленными поворотами и симметриями.

2. Если в абелевой группе (К , +) наряду с операцией сложения + задана ещё одна операция: произведение * (или · ), которая связана с + дистрибутивными законами :

(A+b)*C=(A*C)+(B*C) , a* (B+c)=(A*B)+(A*C) " a,B,C K

и 0*A=A*0=0 " A K,

То К называется Кольцом.

Если в кольце (К, +, *) дополнительно для произведения * выполняется ассоциативный закон, т. е. если

(A* B) *C=A*(B*C) " A,B,C K,

То кольцо называется Ассоциативным. А если кроме того $ единичный элемент 1, т. е. такой, что 1*A = A*1=A " aÎ K, то кольцо называется Унитарным (или кольцом с 1). Если в кольце выполняется коммутативный закон для *, то кольцо называется Коммутативным.

Ассоциативное унитарное кольцо, в котором каждый ненулевой элемент A имеет обратный А-1, т. е. такой, что А*А-1 = А-1*А = 1 называется Телом.

Коммутативное тело называется Полем.

Примеры.

1) ( Z, +, · ) – коммутативное ассоциативное унитарное кольцо.

2) (Q, +, · ), (R, +, · ), (C, +, · ) – поля.

3) K[Х] – множество многочленов с коэффициентами из поля K c обычными операциями сложения и умножения многочленов – коммутативное ассоциативное унитарное кольцо.

4) Булеан (W(U), Å, Ç): нулевой элемент -- Æ, единичный – U, противоположный элемент для множества А – само А, т. к. А Å А = Æ, обратного элемента не существует. Таким образом это -- ассоциативное коммутативное унитарное кольцо.

5) Тело кватернионов. Кватернионами называются выражения вида:

X = A + BI + CJ + DK ,

Где a, b, c, d Î R, и кроме того символы i, j, k Удовлетворяют соотношениям:

I2 = j2 = k2 = -1, ij = - ji = k,

jk = - kj = i,

ki = -Ik= J.

При этом A называется действительной (или скалярной) частью кватерниона X, а BI + cJ + dK -- векторной частью. Два кватерниона складываются так же, как и векторы:

(A1 + B1I + C1J + D1K)+ (A2 + B2I + C2J + D2K) = (A1+ A2) + (B1+ B2)I + (C1+ C2)J + (D1+ D2)K .

Соотношения между базисными элементами i, j, k позволяют естественным образом определить и операцию произведения кватернионов. Но уже из этих соотношений видно, что произведение – не коммутативно. Нетрудно, однако, проверить, что множество кватернионов с выше заданными операциями является телом. В частности обратным к кватерниону X = A + BI + CJ + DK Является кватернион

X-1= .

С помощью кватернионов очень изящно решаются задачи, связанные с композицией поворотов твердого тела в пространстве. Повороту вокруг вектора D = (B, c, d) на угол j поставим в соответствие кватернион a = A + bI + cJ + dK, где A = Cos. Если x = (X, y, z) – вектор, определяющий начальное положение тела, а вектор x’ = (X’, y’, z’) – после поворота, то можно показать, что x' = a-1xa. Если совершается два поворота a и b, то общий результат определяется как произведение ab : x'' = (ab)-1x(ab).

6) Пусть M – натуральное число. На множестве целых чисел определим следующее отношение эквивалентности: , если числа A и b имеют одинаковые остатки при делении на M (свойства рефлексивности, симметричности и транзитивности данного отношения очевидны). Обозначим через = – фактор-множество множества целых чисел Z по введенному отношению эквивалентности.

Определим на операции сложения и умножения определим следующим образом:

и

Можно показать, что определения корректны, т. е. результаты не зависят от выбора представителей классов – элементов A И b. Проверка свойств показывает, что – коммутативное ассоциативное унитарное кольцо.

Если M – составное число, то в этом кольце существуют делители нуля. Пусть M = m1M2 , тогда , отсюда следует, что класс [M1] не имеет обратного (в противном случае получили бы . Значит, в данном случае кольцо классов вычетов не является полем. Но, если M = p – простое число, то – поле.

3. Алгебраические структуры с тремя операциями (и соответствующим набором свойств) называют Алгебрами.

Примеры.

1) Булева алгебра множеств с операциями (дополнение).

2) Алгебра матриц с операциями сложение, умножение и умножение на число.

Алгебраические структуры, на которых помимо операций заданы отношения, называются Алгебраическими системами.

Примером алгебраических систем могут служить решетки. В качестве операций можно рассматривать:

A+B = inf, A · B = sup

4. При изучении данных структур часто не важна природа элементов которые их составляют, а также конкретный смысл операций. В этом случае принято отождествлять алгебраические структуры, между которыми существует биекция, сохраняющая операции (т. е. такое отображение, при котором сумма переходит в сумму, произведение в произведение и т. д.):

Если F : GH – биекция структур (например, колец), причем

F(A + b) = f(A) + f(B) и F(Ab) = f(A) f(B) " a, b,c G,

То F Называется Изоморфизм, а G и H – Изоморфными (в этом случае пишут: GH).

Отношение изоморфности является отношением эквивалентности. Изоморфные структуры отождествляют, считают равными.

< Предыдущая		Следующая >