1.4.4. Отношения частичного порядка
Определение. Бинарное отношение R на множестве А называется Отношением частичного порядка, если оно рефлексивно, транзитивно и антисимметрично. Само множество А при этом называется Частично упорядоченным.
Не следует, однако, думать, что частичная упорядоченность это свойство самого множества. На одном и тои же множестве могут быть заданы разные отношения частичного порядка.
Например, на множестве натуральных чисел N отношением частичного порядка является обычное отношение![]() , а также отношение делимости
, а также отношение делимости ![]() , и вообще любое отношение удовлетворяет свойствам рефлексивности, транзитивности и антисимметричности.
, и вообще любое отношение удовлетворяет свойствам рефлексивности, транзитивности и антисимметричности.
Другие Примеры:
1. На множестве ![]() отношение включения
отношение включения ![]() .
.
2. Отношение “ младше-старше ” на множестве людей.
3. Отношение “начальник-подчиненный” на всяком предприятии.
4. Лексикографический порядок слов в словаре.
Если R - отношение частичного порядка и ARb, то вместо этого пишут A![]() R b или просто A
R b или просто A![]() B. При этом говорят, что A меньше либо равно B. Если при этом дополнительно
B. При этом говорят, что A меньше либо равно B. Если при этом дополнительно ![]() , то пишут А<b и говорят, что А строго меньше B. Говорят также, что А предшествует B.
, то пишут А<b и говорят, что А строго меньше B. Говорят также, что А предшествует B.
Если для элементов ![]() верно, что
верно, что ![]() или
или ![]() , то говорят, что элементы А и B сравнимы. Заметим сразу же, что не всегда любые два элемента сравнимы (возьмем к примеру хотя бы
, то говорят, что элементы А и B сравнимы. Заметим сразу же, что не всегда любые два элемента сравнимы (возьмем к примеру хотя бы ![]() или
или ![]() ) .
) .
Если А<b и не существует элемента Х , такого, что А<х и Х<b, то А называется непосредственно меньшим или непосредственно предшествующим элементу B.
Частично упорядоченные множества (точнее отношения порядка на них) удобно изображать в виде специальных графов, которые называются диаграммами Хассе. Как обычно, элементы данного множества А, b и т. д. изображаются при этом как вершины графа. Но ребрами (без стрелок) соединяются не все пары сравнимых элементов, а только непосредственно меньшие с непосредственно большими, причем, если например A меньше B, то вершина A изображается ниже, чем B.
Примеры.
1. ![]() ( { a, b,c } ),
( { a, b,c } ), ![]() 2. {1,2,3,4}, £
2. {1,2,3,4}, £
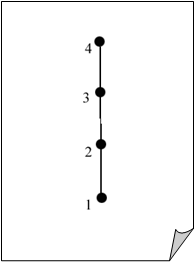
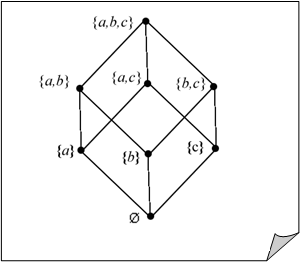
Если элемент A Множества A такой, что ![]()
![]() , то А называется Наибольшим, а если
, то А называется Наибольшим, а если ![]()
![]() , то элемент A Называется Наименьшим.
, то элемент A Называется Наименьшим.
В предшествующих примерах {A, B, C} и “4” -- наибольшие, а Ø и “1” -- наименьшие элементы.
Однако, наибольший и наименьший элементы существуют не всегда. В (Z,![]() ) не существует ни наибольшего ни наименьшего элементов.
) не существует ни наибольшего ни наименьшего элементов.
Нетрудно доказать, что если наибольший (наименьший) элемент существует, то он единственный.
Элемент А называется Максимальным, если ![]() либо
либо ![]() , либо А и Х несравнимы.
, либо А и Х несравнимы.
Элемент А Называется Минимальным, если ![]() либо
либо ![]() , либо А и Х несравнимы.
, либо А и Х несравнимы.
В отличие от наибольшего (наименьшего), максимальных (минимальных) элементов может быть несколько. В N C отношением "A Делит B" Минимальными элементами являются все простые числа, максимальные элементы отсутствуют.
Определение. Отношение R на множестве А называется Отношением линейного порядка, а множество А Линейно упорядоченным, если R является отношением частичного порядка и если R является связанным. (Граф такого отношения представляет собой вертикальную линию).
Линейно упорядоченное множество А называется Вполне упорядоченным, если каждое его непустое подмножество ![]() Имеет наименьший элемент.
Имеет наименьший элемент.
Например, (N, ![]() ) -- вполне упорядочено, а (Z,
) -- вполне упорядочено, а (Z, ![]() ) -- нет.
) -- нет.
Если ![]() , то Верхней (Нижней) гранью множества M называется любой элемент
, то Верхней (Нижней) гранью множества M называется любой элемент ![]() , такой, что
, такой, что ![]() Выполняется условие
Выполняется условие ![]() (
(![]() ). Точной верхней (Sup) (Нижней (Inf)) гранью множества М называется наименьшая верхняя (наибольшая нижняя) грань М.
). Точной верхней (Sup) (Нижней (Inf)) гранью множества М называется наименьшая верхняя (наибольшая нижняя) грань М.
Например, на множестве ![]() с отношением
с отношением ![]() для всякого
для всякого ![]() существуют точные верхняя и нижняя грани. Это, как нетрудно видеть, объединение и пересечение всех множеств из M, соответственно.
существуют точные верхняя и нижняя грани. Это, как нетрудно видеть, объединение и пересечение всех множеств из M, соответственно.
Частично упорядоченное множество А называется Решеткой, если для любых двух элементов ![]() существуют точные верхняя и нижняя грани.
существуют точные верхняя и нижняя грани.
Примеры.
1. Если ![]() , то для любых двух
, то для любых двух ![]()
![]() -- точная нижняя грань, а
-- точная нижняя грань, а ![]() -- точная верхняя грань.
-- точная верхняя грань.
2. Пусть А линейно упорядоченное множество. Тогда оно также является решеткой:
sup{A, b}= Max{A, b}, inf{A, b}= Min{A, b}
3. Рассмотрим N с отношением A | b (A делит B). Тогда
sup{A, b}= НОК(A, b), inf{A, b}= НОД(A, b)
Решетка, в которой sup и inf существуют для любого её подмножества называется Полной.
| < Предыдущая | Следующая > |
|---|