1.4.1. Отношения Основные понятия и способы задания отношений

В математике (а также других науках и сферах деятельности человека) для описания связей между предметами используется понятие отношения.

Например, отношение “меньше - больше” на множестве действительных чисел; отношение делимости на множестве целых чисел; отношение подобия на множестве треугольников; параллельности или перпендикулярности на множестве прямых и плоскостей; отношения родства, дружбы, знакомства на множестве людей; отношение “начальник-подчиненный” на предприятии и др.

Определение. Бинарным отношением на множествах A и B называется всякое подмножество.

Если элементы и находятся в отношении R, то вместо () принято писать ARb . Например, A < B (для отношения “меньше - больше”), (A делится на B, для отношения делимости), ∆ABC~∆KLM (для отношения подобия треугольников) и т. д.

Если B =A , то отношение называется отношением на множестве А

( вместо: отношение на множествах А и А).

Для отношения множество А называется множеством определения, а В -- множеством значений отношения R.

Если R=AB , то отношение R называется универсальным, или всюду истинным. Если R=Ø, То такое отношение называется пустым, или всюду ложным.

Два отношения R1 и R2 называются равными, если R1=R2 как множества. Если (как множества) R1R2, то говорят, что отношение R1 влечет отношение R2 (или из отношения R1 следует отношение R2).

Отношения на числовых множествах удобно иллюстрировать графически в виде соответствующего множества точек на координатной плоскости.

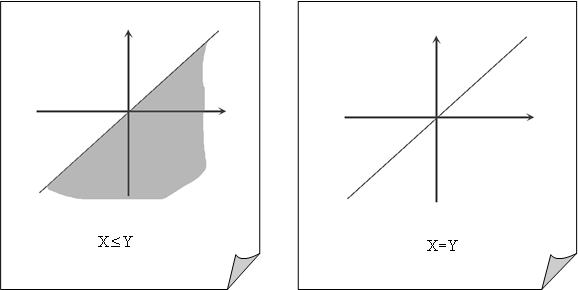Например, отношению “” на множестве действительных чисел R соответствует полуплоскость. Отношению “=” на R соответствует прямая.

Всякое отображение (функцию) F: A→ B Можно рассмотреть как отношение F На множествах А и В , положив Afb, если f(A) = b Для всех aA, bB.

В случае, когда А, ВR графической иллюстрацией такого отношения будет обычный график функции Y=f(x).

Обратно, всякое отношение В Называется функциональным, если единственный элемент , такой, что ARb .

Из рассмотренных примеров видно, что отношения (на числовых множествах) могут быть заданы графически в виде соответствующего множества точек на координатной плоскости.

Отношения на конечных множествах могут быть заданы непосредственным перечислением всех пар элементов, находящихся в данном отношении.

Например, рассмотрим отношение делимости ( ARb, если A, т. е. A делится на B) на множестве А={1; 2; 3; 4; 5; 6}. Тогда R= { (1,1); (2,1); (2,2); (3,1); (3,3); (4,1); (4,2); (4,4); (5,1); (5,5); (6,1); (6,2); (6,3); (6,6) }.

Это же отношение можно задать с помощью матрицы отношения.

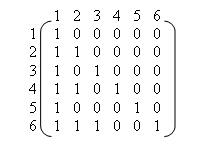Матрицей бинарного отношения , где | А | = N, | B | = m, называется бинарная (N´M)-матрица M = (Mij), в которой Mij =1, если AiRbj; и Mij = 0, в противном случае. Здесь мы считаем, что элементы множеств А и В предварительно пронумерованы и, таким образом, каждому элементу множества А соответствует строка матрицы, а каждому элементу В – столбец.

Для рассматриваемого отношения делимости получаем следующую матрицу: отношение на том же множестве А имеет нижнюю треугольную матрицу (выше диагонали все элементы – нули, а на диагонали и ниже – все элементы равны 1).

Отношение , такое, что = { (A, a) | aR} (по сути это отношение равенства) называется единичным. Оно имеет единичную матрицу.

Еще один способ задания отношений – Графы отношений.

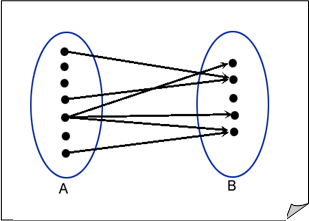Отношение можно представить в виде рисунка, на котором элементам А и В соответствуют точки (вершины графа), при этом если ARb, то вершины A и B соеденены линией (ребром) со стрелкой в направлении от A до B (см. рис. справа).

Если В = А, то на графе соответствующего отношения изображаются только вершины, соответствующие одному множеству А, и соединяются ребрами по тем же правилам.

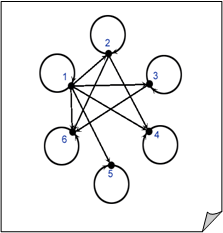Отношение делимости на множестве А = { 1; 2; 3; 4; 5; 6; } имеет следующий граф, изображенный на рисунке справа.

Аналогично определяются n-арные отношения на множествах А1, А2, …, Аn , Как всякие подмножества А1А2 … Аn . При этом если все Ai = А, то соответствующее отношение N называется N-местным отношением на А.

Примеры.

1) Трехместное отношение на R быть сторонами треугольника: (A, b, c)R, если существует треугольник со сторонами A, b, c.

2) Четырехместное отношение на N: (A, b, c, d), если = .

< Предыдущая		Следующая >