1.4.2. Операции над бинарными отношениями и их свойства
Поскольку отношения (по определению) представляют собой множества, то для них можно рассматривать все операции, действующие на множествах. При этом сохраняются все их свойства.
Рассмотрим специальные операции.
Пусть имеются отношения R1![]() , R2
, R2![]() . Произведением отношений R1 и R2 называется отношение R1R2
. Произведением отношений R1 и R2 называется отношение R1R2![]() , такое, что AR1R2C
, такое, что AR1R2C![]() Тогда и только тогда, когда AR1B и BR2C для некоторого B
Тогда и только тогда, когда AR1B и BR2C для некоторого B![]() .
.
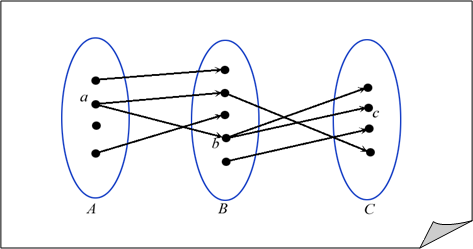 |
Если разместить на одном рисунке графы обоих отношений, то AR1R2C означает, что от элемента A двигаясь по ребрам в направлении стрелок можно перейти к элементу С.
Понятно, что, вообще говоря, R1R2![]() R2R1, даже если оба произведения определены. Таким образом, произведение отношение не обладает свойством коммутативности. Однако, нетрудно показать, что она является ассоциативным:
R2R1, даже если оба произведения определены. Таким образом, произведение отношение не обладает свойством коммутативности. Однако, нетрудно показать, что она является ассоциативным:
· ( R1R2) R3 = R1 (R2R3).
Пусть ![]() . Отношение R-1
. Отношение R-1![]() , такое, что R-1={(B, a)|
, такое, что R-1={(B, a)| ![]() }, называется Обратным К отношению R.
}, называется Обратным К отношению R.
Легко также видеть, что
· ( R-1)-1 = R.
· ( R1R2)-1 =R1-1R2-1.
Отметим также следующие свойства, которые часто проверяются при исследовании тех или иных отношений.
Определение. Бинарное отношение R на множестве А называется
- Рефлексивным, если ![]() ARa , (матрица такого отношения имеет 1 на всех диагональных местах, а граф – петли при каждой вершине);
ARa , (матрица такого отношения имеет 1 на всех диагональных местах, а граф – петли при каждой вершине);
- Симметричным, если ![]() из ARb следует BRa (матрица симметрична, граф изображают без стрелок);
из ARb следует BRa (матрица симметрична, граф изображают без стрелок);
- Транзитивным, если ![]() из ARb и BRc следует ARc.
из ARb и BRc следует ARc.
Наряду с вышеперечисленными свойствами рассматриваются также следующие:
Отношение называется
- Антирефлексивным, если ![]() (A, a)
(A, a)![]() R;
R;
- Антисимметричным, если ![]() из (A, b)
из (A, b)![]() следует (B, a)
следует (B, a)![]() (т. е., что то же самое, если из ARb и BRa следует A=b);
(т. е., что то же самое, если из ARb и BRa следует A=b);
- Связанным, если ![]() выполняется ARb Или bRa.
выполняется ARb Или bRa.
| < Предыдущая | Следующая > |
|---|