1.1.3. Операции над множествами

Во всех рассуждениях о нескольких множествах удобно считать, что они являются подмножествами некоторого более широкого множества U, которое называется Универсальным. На практике, как правило, универсальное множество даже явно не указывается, а ясно из контекста, или в случае необходимости может быть легко установлено.

Определение 1. Пересечением двух множеств A и B Называется множество A ÇB, состоящее из элементов, которые принадлежат каждому из множеств A и B, т. е.

Например, {1; 2; 5; 7} Ç {1; 5; 6} = {1; 5}. Пересечением множества прямоугольников с множеством ромбов является множество квадратов. Пересечением множества студентов-первокурсников с множеством отличников является множество первокурсников-отличников.

Определение 2. Объединением множеств A и B называется множество AÈB, состоящее из элементов, которые принадлежат хотя бы одному из множеств A или B:

Например, {1; 2; 5} È {1; 5; 6; 7} = {1; 2; 5; 6; 7}.

Аналогично определяются операции объединения и пересечения трех, четырех, любой совокупности множеств. При этом используются следующие обозначения.

Если S = {A1, A2, …} — совокупность множеств, то их объединение и пересечение обозначаются: , ; или , -- для конечных совокупностей и , — для бесконечных совокупностей; а также , , где I — некоторое множество индексов.

Определение 3. Разностью множеств A и B называется множество A \ B, состоящее из всех элементов множества A, не принадлежащих множеству B :

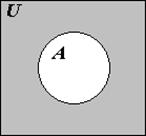
Если ясно, о каком универсальном множестве U идет речь, то разность U \ A называется дополнением множества A и обозначается: .

Например, разностью множества четных чисел и множества чисел, кратных 3, является множество четных чисел, не делящихся на 6. Дополнением множества четных чисел в (универсальном множестве целых чисел) является множество нечетных чисел.

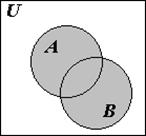
Диаграммы Эйлера-Венна.

Введенные операции допускают удобное графическое истолкование с помощью диаграмм (или кругов) Эйлера-Венна, где результат операции указан штриховкой:

< Предыдущая		Следующая >