99. Разложение многочлена на множители
Определение. Функция вида F(X)![]() называется Целой рациональной функцией от Х.
называется Целой рациональной функцией от Х.
Теорема Безу. (Этьенн Безу (1730 – 1783) – французский математик)
При делении многочлена F(X) на разность X – A Получается остаток, равный F(A).
Доказательство. При делении многочлена F(X) на разность X – A Частным будет многочлен F1(X) степени на единицу меньшей, чем F(X), А остатком – постоянное число R.
![]()
Переходя к пределу при Х ® A, Получаем F(A) = R.
Следствие. Если, а – корень многочлена, т. е. F(A) = 0, то многочлен F(X) делится на (х – а) без остатка.
Определение. Если уравнение имеет вид Р(х) = 0, где Р(х) – многочлен степени N, то это уравнение называется Алгебраическим уравнением степени N.
Теорема. (Основная теорема алгебры) Всякая целая рациональная функция F(X) имеет, по крайней мере, один корень, действительный или комплексный.
Теорема. Всякий многочлен N – ой степени разлагается на N Линейных множителей вида (X – A) и множитель, равный коэффициенту при Xn.
Теорема. Если два многочлена тождественно равны друг другу, то коэффициенты одного многочлена равны соответствующим коэффициентам другого.
Если среди корней многочлена встречаются кратные корни, то разложение на множители имеет вид:
![]()
![]()
Ki - кратность соответствующего корня.
Отсюда следует, что Любой многочлен N – ой степени имеет ровно N корней (действительных или комплексных).
Это свойство имеет большое значение для решения алгебраических уравнений, дифференциальных уравнений и играет важную роль в анализе функций.
Рассмотрим несколько примеров действий с комплексными числами.
Пример. Даны два комплексных числа ![]() . Требуется а) найти значение выражения
. Требуется а) найти значение выражения 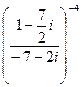 В алгебраической форме, б) для числа
В алгебраической форме, б) для числа ![]() найти тригонометрическую форму, найти Z20, найти корни уравнения
найти тригонометрическую форму, найти Z20, найти корни уравнения ![]()
A) Очевидно, справедливо следующее преобразование:
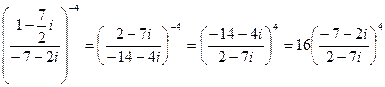
Далее производим деление двух комплексных чисел:
![]()
Получаем значение заданного выражения: 16(-I)4 = 16I4 =16.
Б) Число ![]() представим в виде
представим в виде ![]() , где
, где
![]()
Тогда ![]() .
.
Для нахождения ![]() воспльзуемся формулой Муавра.
воспльзуемся формулой Муавра.
![]()
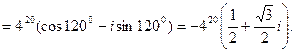
Если ![]() , то
, то ![]()
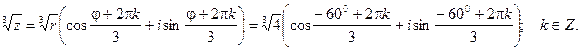
| < Предыдущая | Следующая > |
|---|