98. Показательная форма комплексного числа

Рассмотрим показательную функцию

Можно показать, что функция W может быть записана в виде:

Данное равенство называется Уравнением Эйлера. Вывод этого уравнения будет рассмотрен позднее. (См. ).

Для комплексных чисел будут справедливы следующие свойства:

1)

2)

3) где M – целое число.

Если в уравнении Эйлера показатель степени принять за чисто мнимое число (Х=0), то получаем:

Для комплексно – сопряженного числа получаем:

Из этих двух уравнений получаем:

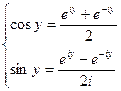
Этими формулами пользуются для нахождения значений степеней тригонометрических функций через функции кратных углов.

Если представить комплексное число в тригонометрической форме:

И воспользуемся формулой Эйлера:

Полученное равенство и есть Показательная форма комплексного числа.

< Предыдущая		Следующая >