80. Число е

Рассмотрим последовательность {xn} = .

Если последовательность {xn} монотонная и ограниченная, то она имеет конечный предел.

По формуле бинома Ньютона:

Или, что то же самое

Покажем, что последовательность {xn} – возрастающая. Действительно, запишем выражение xn+1 и сравним его с выражением xn:

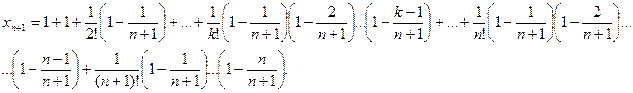Каждое слагаемое в выражении xn+1 больше соответствующего значения xn, и, кроме того, у xn+1 добавляется еще одно положительное слагаемое. Таким образом, последовательность {xn} возрастающая.

Докажем теперь, что при любом n ее члены не превосходят трех: xn < 3.

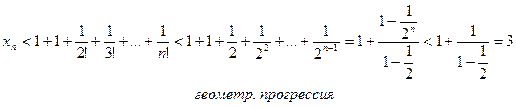
Итак, последовательность 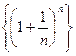- монотонно возрастающая и ограниченная сверху, т. е. имеет конечный предел. Этот предел принято обозначать буквой е.

Из неравенства следует, что е £ 3. Отбрасывая в равенстве для {xn} все члены, начиная с четвертого, имеем:

Переходя к пределу, получаем

Таким образом, число е заключено между числами 2,5 и 3. Если взять большее количество членов ряда, то можно получить более точную оценку значения числа е.

Можно показать, что число е иррациональное и его значение равно 2,71828…

Аналогично можно показать, что , расширив требования к х до любого действительного числа:

Предположим:

Найдем

Число е является основанием натурального логарифма.

Выше представлен график функции y = lnx.

< Предыдущая		Следующая >