81. Связь натурального и десятичного логарифмов
Пусть х = 10у, тогда lnx = ln10y, следовательно lnx = yln10
у = 
, где М = 1/ln10 » 0,43429…- модуль перехода.
y f(x)
A + e
A
A - e
0 a - D a a + D x
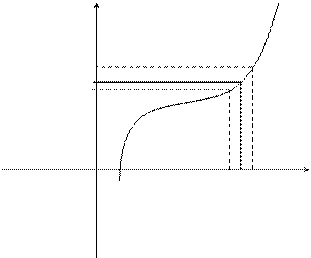
Пусть функция f(x) определена в некоторой окрестности точки х = а (т. е. в самой точке х = а функция может быть и не определена)
Определение. Число А называется Пределом функции f(x) при х®а, если для любого e>0 существует такое число D>0, что для всех х таких, что
0 < ïx - aï < D
Верно неравенство ïf(x) - Aï< e.
То же определение может быть записано в другом виде:
Если а - D < x < a + D, x ¹ a, то верно неравенство А - e < f(x) < A + e.
Запись предела функции в точке: 
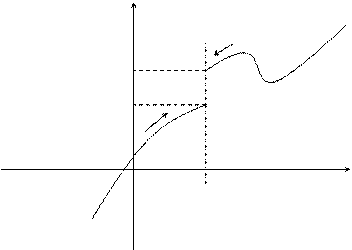
Определение. Если f(x) ® A1 при х ® а только при x < a, то 
- называется Пределом функции f(x) в точке х = а Слева, а если f(x) ® A2 при х ® а только при x > a, то 
называется Пределом функции f(x) в точке х = а Справа.
у
f(x)
А2
А1
0 a x
Приведенное выше определение относится к случаю, когда функция f(x) не определена в самой точке х = а, но определена в некоторой сколь угодно малой окрестности этой точки.
Пределы А1 и А2 называются также Односторонними пределами функции f(x) в точке х = а. Также говорят, что А – Конечный предел функции f(x).
| < Предыдущая | Следующая > |
|---|
