78. Ограниченные и неограниченные последовательности

Определение. Последовательность {xn} называется Ограниченной, если существует такое число М>0, что для любого n верно неравенство:

Т. е. все члены последовательности принадлежат промежутку (-М; M).

Определение. Последовательность {xn}называется Ограниченной сверху, если для любого n существует такое число М, что

Xn £ M.

Определение. Последовательность {xn}называется Ограниченной снизу, если для любого n существует такое число М, что

Xn ³ M

Пример. {xn} = n – ограничена снизу {1, 2, 3, … }.

Определение. Число А называется Пределом последовательности {xn}, если для любого положительного e>0 существует такой номер N, что для всех n > N выполняется условие:

Это записывается: lim xn = a.

В этом случае говорят, что последовательность {xn}Сходится к а при n®¥.

Свойство: Если отбросить какое - либо число членов последовательности, то получаются новые последовательности, при этом если сходится одна из них, то сходится и другая.

Пример. Доказать, что предел последовательности lim .

Пусть при n > N верно 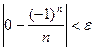, т. е. . Это верно при , таким образом, если за N взять целую часть от , то утверждение, приведенное выше, выполняется.

Пример. Показать, что при n®¥ последовательность 3, имеет пределом число 2.

Итого: {xn}= 2 + 1/n; 1/n = xn – 2

Очевидно, что существует такое число n, что , т. е. lim {xn} = 2.

Теорема. Последовательность не может иметь более одного предела.

Доказательство. Предположим, что последовательность {xn}имеет два предела a и b, не равные друг другу.

Xn ® a; xn ® b; a ¹ b.

Тогда по определению существует такое число e >0, что

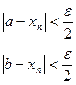
Запишем выражение:

А т. к. e - Любое Число, то , т. е. a = b. Теорема доказана.

Теорема. Если Xn ® A, то .

Доказательство. Из Xn ® A следует, что . В то же время:

, т. е. , т. е. . Теорема доказана.

Теорема. Если Xn ® A, то последовательность {Xn} ограничена.

Следует отметить, что обратное утверждение неверно, т. е. из ограниченности последовательности не следует ее сходимость.

Например, последовательность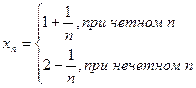Не имеет предела, хотя

< Предыдущая		Следующая >