77. Введение в математический анализ. Числовая последовательность

Определение. Если каждому натуральному числу n поставлено в соответствие число хn, то говорят, что задана Последовательность

X1, х2, …, хn = {xn}

Общий элемент Последовательности является функцией от n.

Xn = f(n)

Таким образом последовательность может рассматриваться как функция.

Задать последовательность можно различными способами – главное, чтобы был указан способ получения любого члена последовательности.

Пример. {xn} = {(-1)n} или {xn} = -1; 1; -1; 1; …

{xn} = {sinpn/2} или {xn} = 1; 0; 1; 0; …

Для последовательностей можно определить следующие Операции:

1) Умножение последовательности на число m: m{xn} = {mxn}, т. е. mx1, mx2, …

2) Сложение (вычитание) последовательностей: {xn} ± {yn} = {xn ± yn}.

3) Произведение последовательностей: {xn}×{yn} = {xn×yn}.

4) Частное последовательностей: 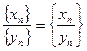при {yn} ¹ 0.

< Предыдущая		Следующая >