46. Функциональные ряды

Определение. Частными (частичными) суммами функционального ряда называются функции

Определение. Функциональный ряд Называется Сходящимся в точке (Х=х0), если в этой точке сходится последовательность его частных сумм. Предел последовательности называется Суммой Ряда в точке Х0.

Определение. Совокупность всех значений Х, для которых сходится ряд Называется Областью сходимости Ряда.

Определение. Ряд Называется Равномерно сходящимся на отрезке [a, b], если равномерно сходится на этом отрезке последовательность частных сумм этого ряда.

Теорема. (Критерий Коши равномерной сходимости ряда)

Для равномерной сходимости ряда Необходимо и достаточно, чтобы для любого числа E>0 существовал такой номер N(E), что при N>N и любом целом P>0 неравенство

Выполнялось бы для всех х на отрезке [A,B].

Теорема. (Признак равномерной сходимости Вейерштрасса)

(Карл Теодор Вильгельм Вейерштрасс (1815 – 1897) – немецкий математик)

Ряд Сходится равномерно и притом абсолютно на отрезке [A,B], если модули его членов на том же отрезке не превосходят соответствующих членов сходящегося числового ряда с положительными членами :

Т. е. имеет место неравенство:

.

Еще говорят, что в этом случае функциональный ряд Мажорируется Числовым рядом .

Пример. Исследовать на сходимость ряд .

Так как всегда, то очевидно, что .

При этом известно, что общегармонический ряд при a=3>1 сходится, то в соответствии с признаком Вейерштрасса исследуемый ряд равномерно сходится и притом в любом интервале.

Пример. Исследовать на сходимость ряд .

На отрезке [-1,1] выполняется неравенство 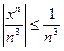т. е. по признаку Вейерштрасса на этом отрезке исследуемый ряд сходится, а на интервалах (-µ, -1) È (1, µ) расходится.

< Предыдущая		Следующая >