45. Функциональные последовательности
Определение. Если членами ряда будут не числа, а функции от Х, то ряд называется Функциональным.
Исследование на сходимость функциональных рядов сложнее исследования числовых рядов. Один и тот же функциональный ряд может при одних значениях переменной Х сходиться, а при других – расходиться. Поэтому вопрос сходимости функциональных рядов сводится к определению тех значений переменной Х, при которых ряд сходится.
Совокупность таких значений называется Областью сходимости.
Так как пределом каждой функции, входящей в область сходимости ряда, является некоторое число, то пределом функциональной последовательности будет являться некоторая функция:
![]()
Определение. Последовательность {Fn(X)} Сходится к функции F(X) на отрезке [a, b], если для любого числа e>0 и любой точки Х из рассматриваемого отрезка существует номер N = N(e, x), такой, что неравенство
![]()
Выполняется при n>N.
При выбранном значении e>0 каждой точке отрезка [a, b] соответствует свой номер и, следовательно, номеров, соответствующих всем точкам отрезка [a, b], будет бесчисленное множество. Если выбрать из всех этих номеров наибольший, то этот номер будет годиться для всех точек отрезка [a, b], т. е. будет общим для всех точек.
Определение. Последовательность {Fn(X)} Равномерно сходится к функции F(X) на отрезке [a, b], если для любого числа e>0 существует номер N = N(e), такой, что неравенство
![]()
Выполняется при n>N для всех точек отрезка [a, b].
Пример. Рассмотрим последовательность ![]()
Данная последовательность сходится на всей числовой оси к функции F(X)=0, т. к.
![]()
Построим графики этой последовательности:
![]() Sinx
Sinx ![]()
![]()
![]()
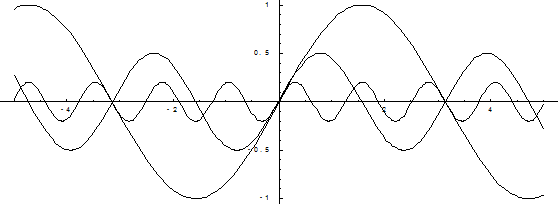
Как видно, при увеличении числа N график последовательности приближается к оси Х.
При использовании компьютерной версии “Курса высшей математики” возможно запустить программу, которая исследует на сходимость знакочередующиеся ряды и определяет характер сходимости. Достаточно ввести общий член ряда и множитель, определяющий знак и нажать Enter. Все рассмотренные выше признаки будут проверены по очереди.
 |
Для запуска программы дважды щелкните на значке:
Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (Ó Waterloo Maple Inc.) любой версии, начиная с Maple V Release 4.
| < Предыдущая | Следующая > |
|---|