Лекция №12. Свойства собственных векторов. Диагонализация матрицы. Сопряжение и Эрмитов операторы и их свойства. Унитарный оператор. Квадратичные формы.
(1) Теорема 20: если собственные значения линейного оператора различны 
попарно, то соответствующие собственные векторы линейно независимы.
Доказательство(метод математической индукции):
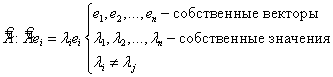
1) 
2) 
3) 
1. Рассмотрим один вектор 
Докажем, что 
линейно независим.
2. . Пусть векторы 
- линейно независимы.
3. . Докажем, что 
- линейно независимы.
Рассмотрим 
1. Умножим на 
2. Подействуем оператором 
По условию 2: 
- линейно независимы.
Так как 
, то 
Возвращаясь к началу условия 3 имеем:
ч. т. д.
Диагонализация.
Пусть оператор 
- спектр линейного оператора.
И , тогда 
- линейно независимы по теореме 20.
Выберем базисом в 
совокупность собственных векторов 
Если 
- базис в :
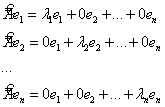
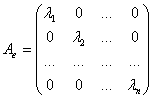
Теорема 21:
Если все корни характеристического уравнения различны, то матрица линейного оператора в базисе из собственных векторов имеет диагональный вид. В противном случае 
матрица будет иметь Жорданову форму.
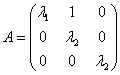
(2) Определение: оператор 
называется сопряжённым по отношению к оператору , если 
Теорема 22: сопряжённый оператор существует для каждого оператора и причём только один.
Доказательство: предположим, что - существует. Тогда согласно определению 
.
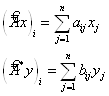
Матрица 
называется сопряжённой по отношению к матрице 
, причём 
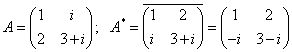
- это Эрмитово сопряжение.
- это комплексное сопряжение.
Свойства Эрмитова сопряжения на матрицах.
1) 
2) 
3) 
4) 
Определение: оператор называется эрмитовым, если 
или 
Если - вещественно, то 
. 
эрмитовость 
сопряжённость
Если 
, то - антиэрмитова.
| < Предыдущая | Следующая > |
|---|
