Лекция №11. Ядро и образ линейного оператора. Инвариантное подпространство. Собственные вектора и собственные значения линейного оператора. Спектр линейного оператора. Подобные матрицы. Свойства собственных векторов.

(1) Образ

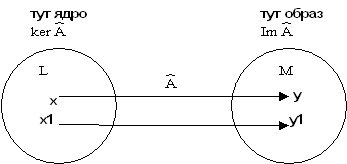
Определение: множество векторов вида , где называется образом линейного оператора .

Свойство 4: - подпространство в .

Докажем: пусть и , тогда и ,

Если и , то и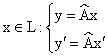

Тогда если , то

Теорема 18: пусть и - подпространства в :

Тогда и

Доказательство: Пусть - базис в и - базис в ,

- базис в ,

Определим оператор следующим образом:

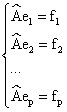
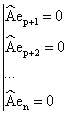
Рассмотрим некоторый вектор

, то

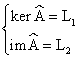
Свойство 5

А) имеет место

Б) если , то есть , то и

В) если , то

2)   Если , то у существует .

(2) Рассмотрим - подпространство.

Определение: называется инвариантным подпространством в относительно действия оператора , если

Если , то и образ также

Примеры:

1)   является инвариантным подпространством в относительно . инвариантно.

2)   Всё пространство является инвариантным подпространством. по определению.

3)   нуль мерное пространство . .

Рассмотрим одномерное инвариантное подпространство.

Рассмотрим вектор - линейная оболочка.

и , то , тогда - инвариантное подпространство.

Определение: вектор называется собственным вектором оператора , а - число, собственное значение данного вектора .

Теорема 19: всякий линейный оператор имеет по крайней мере один собственный вектор.

Доказательство: предположим, что собственный вектор существует. Тогда

- матричное представление оператора .

- система однородных линейных уравнений .

Условие существования нетривиального решения: - характеристическое уравнение.

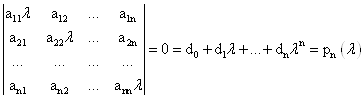
- характеристический полином.

Согласно основное теоремы алгебры уравнение имеет по крайней мере одно решение, корень.

- корень

и

- нетривиальное решение.

- существует.

Определение: множество собственных значений оператора называется его спектром.

Определение: Матрицы и называются подобными, если существует матрицы невырожденная.

- матрицы подобны

(теорема 17)

Свойства подобных матриц.

1)  

2)  

3)  

У подобных матриц спектры совпадают.

< Предыдущая		Следующая >