Лекция №10. Операции над линейными операторами. Матрица линейного оператора и её преобразование. Ядро и образ линейного оператора.

(1) Оператор

1.   Сложение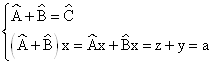

2.   Умножение на числа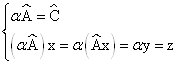

3.   Умножение операторов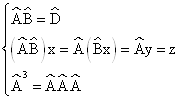

Свойства:

1)  

2)  

3)  

4)  

5)  

6)  

7)  

8)  

9)  

Свойства 1-8 соответствуют аксиомам линейного пространства, следовательно множество линейных операторов образует линейное пространство.

(2) Матрица линейного оператора и её преобразование.

(преобразование)

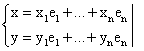- разложение по базису.

Определим: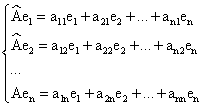

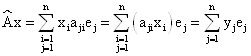
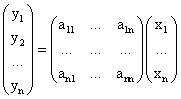
Всякому линейному оператору в некотором базисе соответствует матрица .

(матричное представление линейного оператора)

Пусть в заданы 2 базиса:

- старый базис.

- новый базис.

или

- матрица перехода от старого базиса к новому.

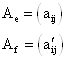
Рассмотрим

:

Теорема 17: матрицы и связаны соотношением . - матрица перехода от базиса к .

Доказательство: рассмотрим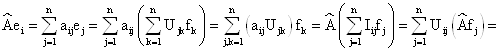

(3) Для каждого оператора существуют понятия, как:

Ядро: - Это подпространства в и .

Образ: -

Определение: множество тех векторов , для которых называется ядром линейного оператора.

, если .

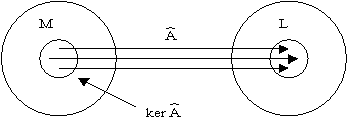
Свойство 1: ядро линейного оператора образует линейное пространство в .

Пусть , то есть .

Тогда , поскольку

Свойство 2

Однородная система уравнений.

Пусть - векторы фундаментальной системы решений.

Фундаментальная система решений есть базис ядра .

Свойство 3: если

То у существует

Решение тривиальное, когда или .

Тогда существует

Свойство 4: Рассмотрим и

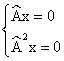
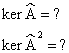
Пример:

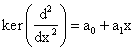
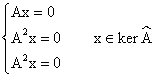
< Предыдущая		Следующая >