Лекция №09. Ортогональный базис и его свойства. Матрица Грама и её определитель. Метод ортогонализации Грама-Шмидта. Линейный оператор. Операции и свойства.
5) Определение: базис ![]() в L называется ортогональным, если векторы
в L называется ортогональным, если векторы ![]() попарно ортогональны, то есть
попарно ортогональны, то есть ![]()
Пример: 
Теорема 14: Если векторы ![]() попарно ортогональны, то они являются линейно независимыми.
попарно ортогональны, то они являются линейно независимыми.
Доказательство: Пусть ![]()
Докажем, что они линейно независимы.
![]() (нулевая линейная комбинация)
(нулевая линейная комбинация)
Умножим скалярно на ![]() последовательно:
последовательно:
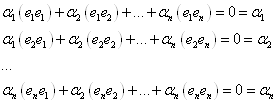
![]() (так как все
(так как все ![]() ) все вектора линейно независимы.
) все вектора линейно независимы.
Свойства ортогонального базиса.
Пусть ![]() - ортогональный базис.
- ортогональный базис.
1) ![]() и
и ![]()

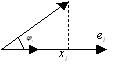
2) 
Если ![]() , то
, то ![]()
Если ![]() , то
, то ![]() ;
; ![]() - общий вид задания скалярного базиса в неортогональном базисе.
- общий вид задания скалярного базиса в неортогональном базисе.
(2) Матрица Грама.
Рассмотрим совокупность векторов ![]() . Поставим вопрос о линейной независимости этих векторов.
. Поставим вопрос о линейной независимости этих векторов.
Образуем ![]() - скалярное произведение.
- скалярное произведение.
 - матрица Грама.
- матрица Грама.
Теорема 15: Для того, чтобы векторы ![]() были линейно независимы, достаточно, чтобы
были линейно независимы, достаточно, чтобы ![]()

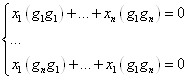
Однородная система уравнений ![]()
![]() - у неё существует только нетривиальное решение при условии, что
- у неё существует только нетривиальное решение при условии, что ![]() ;
; ![]() .
.
Если ![]() , то у
, то у ![]() существует нетривиальное решение, следовательно
существует нетривиальное решение, следовательно ![]() - линейно независимы.
- линейно независимы.
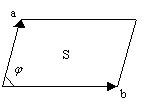
Геометрический смысл определителя Грама.
Рассмотрим: ![]()
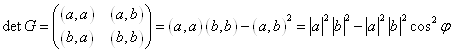
![]() - площадь параллелограмма.
- площадь параллелограмма.
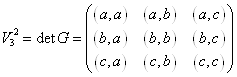
![]() - Объём N-мерного параллелепипеда.
- Объём N-мерного параллелепипеда.
(3) Метод ортогонализации Грама-Шмидта.
Любой базис можно ортогонализовать.
Теорема 16: в любом евклидовом пространстве существует ортогональный базис.
Доказательство: пусть ![]() - базис в L
- базис в L
1) Пусть ![]() ,
, ![]()
2) Пусть ![]()
![]()
![]()
![]()
3) Пусть ![]()
![]()
![]()
K) ![]()
![]()
(4) Линейный оператор
Оператор: Преобразование - Тождественно
Отображение -
Функционал -
Функция -
...
Рассмотрим L и M - линейные пространства.
![]()
Для любого ![]() найдём по некоторому правилу
найдём по некоторому правилу ![]() . Это правило и есть оператор.
. Это правило и есть оператор.
Определение: если для любого ![]() ставится соответствие по некоторому правилу
ставится соответствие по некоторому правилу ![]() , то говорят, что на множестве
, то говорят, что на множестве ![]() задан оператор
задан оператор ![]() со значениями в
со значениями в ![]() .
.
![]() , если
, если ![]()
Определение: оператор ![]() называется линейным, если он удовлетворяет двум условиям линейности:
называется линейным, если он удовлетворяет двум условиям линейности:
1) ![]()
2) ![]()
![]() - образ множества
- образ множества ![]()
![]() - прообраз множества
- прообраз множества ![]()
Если ![]() , то
, то ![]() называется преобразованием.
называется преобразованием.
![]() - преобразование
- преобразование ![]() самого в себя при действии
самого в себя при действии ![]()
![]()
![]()
![]() - матрица
- матрица ![]()
![]() - столбцы
- столбцы ![]()
![]()
| < Предыдущая | Следующая > |
|---|