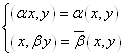Лекция №08. Скалярное произведение. Примеры. Евклидово пространство. Неравенство Коши-Буняковского. Длина, угол. Нормированное пространство.Ортогональность и ортогональный базис. Матрица Грама.

Свойства решений систем уравнений.

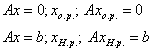
1)   ; - Частное решение, .

2)   Пусть - есть два частных решения.

1)   В L определены:

Определение: в линейном пространстве L задано скалярное произведение, если в каждой паре ставится в соответствие число, обозначаемое и удовлетворяющее условиям (аксиомам):

В вещественном L	В комплексном L
1)   2)   ; 3)   4)	1)   - комплексное сопряжение. 2)   3)   4)

Определение: линейное пространство, в котором задано скалярное произведение, называется евклидовым.

Примеры:

1)  

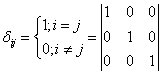
2)  

3)  

А)

Б) Общий вид задания скалярного произведения.

- матрица

Вторая и третья аксиомы выполняются.

Первая аксиома:

- симметричная матрица.

Четвёртая аксиома.

- квадратичная форма

- Она определяет положительно определённую квадратичную форму.

A: 1)

2)  

3)  

3) - Комплексное линейное пространство.

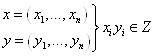
А)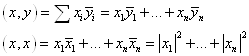

Б) Общий вид

Первая аксиома:

- операция Эрмитово сопряжение.

A: 1)

2)  

3)  

4)  

А) = число

Б)

- функция распределение (весовая функция).

2)   Неравенство Коши-Буняковского.

Доказательство:

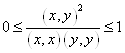
- длина (норма) вектора.

(определение)

< Предыдущая		Следующая >