Лекция №07. Формула Крамера. Фундаментальная система решений. Общее решение. Свойства решений. Скалярное произведение. Евклидово пространство.
Теорема 12 (Кроникера-Капелли): Для того, чтобы система уравнений ![]() была совместной, необходимо и достаточно, чтобы
была совместной, необходимо и достаточно, чтобы ![]() .
.
Доказательство (необходимость):
Пусть система совместна. Докажем, что ![]() .
.
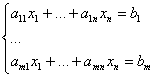
![]()
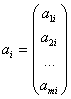
![]() - линейная комбинация строк матрицы А.
- линейная комбинация строк матрицы А.
Так как система совместна, то существует её решение ![]()
![]() - решения.
- решения.
![]()
![]() Столбец
Столбец ![]() есть некоторая линейная комбинация столбцов матрицы А, то если
есть некоторая линейная комбинация столбцов матрицы А, то если ![]() , то и
, то и ![]() .
.
Доказательство (достаточность):
1) Пусть ![]() .
.
2) Докажем, что система совместна.
Итак, ![]() .
.
![]()
![]() базисных столбцов в А являются базисными столбцами и для матрицы А.
базисных столбцов в А являются базисными столбцами и для матрицы А.
![]() вполне конкретны, следовательно, система совместна.
вполне конкретны, следовательно, система совместна.
1) Формула Крамера.
Рассмотрим: ![]() , где А - квадратная,
, где А - квадратная, ![]() .
.
Пусть ![]()
Тогда ![]() и равен
и равен ![]() , следовательно, система совместна и определённа.
, следовательно, система совместна и определённа.
Существует ![]() . Тогда
. Тогда ![]()
![]()
![]()

2) Фундаментальная система решений - это совокупность частных линейно независимых решений.
Рассмотрим: ![]() - однородная система уравнений.
- однородная система уравнений.
1) ![]() - всегда совместна.
- всегда совместна.
2) Всегда существует нулевое ![]() или тривиальное решение.
или тривиальное решение.
Теорема 13: Однородная система уравнений ![]() с
с ![]() неизвестными имеет нетривиальное (ненулевое) решение тогда и только тогда, когда
неизвестными имеет нетривиальное (ненулевое) решение тогда и только тогда, когда ![]()
Доказательство:
Рассмотрим: ![]() .
. ![]() . Имеем задачу на определение линейной зависимости столбцов матрицы А. Если столбцы
. Имеем задачу на определение линейной зависимости столбцов матрицы А. Если столбцы ![]() Линейно зависимы, то существует
Линейно зависимы, то существует ![]() . Тогда это
. Тогда это ![]() - решение
- решение ![]() . Так как
. Так как ![]() линейно зависимы, то
линейно зависимы, то ![]()
Фундаментальная система решений.
Пример 1:
![]()
![]() ;
; ![]()
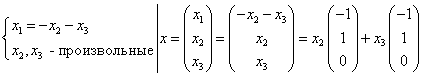
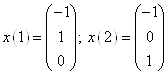 - Частные решения.
- Частные решения. ![]()

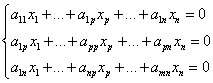
![]() . Значит существует нетривиальное решение. Найдём в матрице А базисный минор:
. Значит существует нетривиальное решение. Найдём в матрице А базисный минор:
![]()
![]()
![]() - линейная комбинация базисных столбцов матрицы А.
- линейная комбинация базисных столбцов матрицы А.
![]() - линейно независимы.
- линейно независимы.
![]()
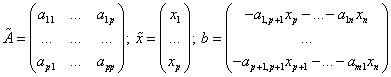
![]()
![]() - решение в общем виде.
- решение в общем виде.
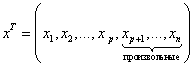
![]()
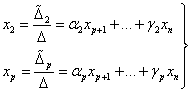 - решение.
- решение.
Найдём частное решение:
 ; N-p случаев.
; N-p случаев.
 N-p частных линейно независимых решений.
N-p частных линейно независимых решений.
Определение: Совокупность частных линейно независимых решений образуют фундаментальную систему решений.
![]()
Определение: общее (полное решение ![]() представляет собой всевозможные линейные комбинации фундаментальной системы решений.
представляет собой всевозможные линейные комбинации фундаментальной системы решений.
![]()
![]() - линейная оболочка.
- линейная оболочка.
О. Р. - однородное(или общее) решение.
![]()
![]()
Свойства:
1) ![]() , то
, то ![]() - неоднородное решение.
- неоднородное решение.
![]() , то
, то ![]() - однородное решение.
- однородное решение.
![]()
Ч. Р. - частное решение.
![]() - частное (любое) решение неоднородного уравнения.
- частное (любое) решение неоднородного уравнения.
Общее решение неоднородной системы уравнений равно сумме решения однородной системы уравнений и любого частного решения неоднородной системы уравнений.
| < Предыдущая | Следующая > |
|---|