Лекция №06. Операции над линейными пространствами. Изоморфизм линейных пространств. Преобразование базиса и преобразование координат. Системы линейных уравнений. Теорема Кроникера-Капелли. Формула Крамера.
(1) Объединение и пересечение линейных пространств.
![]() - линейные пространства.
- линейные пространства.
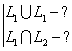
![]() - конечные множества.
- конечные множества.
![]() - число элементов в этих множествах.
- число элементов в этих множествах.
![]()
Теорема 10: Пусть ![]() - линейные пространства. Тогда
- линейные пространства. Тогда ![]() или
или ![]() .
.
Доказательство: Пусть ![]() .
.
Тогда:
![]() - базис в
- базис в ![]()
![]() - базис в
- базис в ![]()
Рассмотрим ![]()
![]() - базис в
- базис в ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Если ![]() (входит), то
(входит), то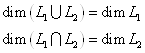
Изоморфизм линейных пространств.
Тезис: пространства одинаковой размерности неотличимы.
Пример: ![]()
![]()
![]()
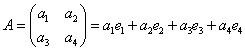
![]() - полином степени 3.
- полином степени 3.
Определение: пространства ![]() и
и ![]() Называются изоморфными, если между векторами
Называются изоморфными, если между векторами ![]() и
и ![]() можно установить взаимно однозначное соответствие, причём должны выполняться следующие условия: если
можно установить взаимно однозначное соответствие, причём должны выполняться следующие условия: если ![]() , то
, то
1) ![]()
2) ![]()
![]()
![]() - отображение, то есть это то соответствие, которое установлено.
- отображение, то есть это то соответствие, которое установлено.
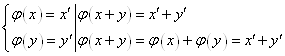
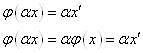
![]() - линейное отображение.
- линейное отображение.
Теорема 11: Если ![]() , то
, то ![]() и
и ![]() изоморфны.
изоморфны.
Доказательство: Пусть ![]() - базис в
- базис в![]() ,
, ![]() - базис в
- базис в ![]() . Тогда выберем
. Тогда выберем ![]() и
и ![]() :
:
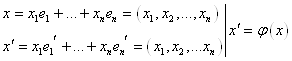
![]() - в
- в ![]() выбираем соответствие
выбираем соответствие ![]() , значит координаты вектора определены однозначно.
, значит координаты вектора определены однозначно.
2) Рассмотрим в пространстве L два базиса:
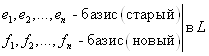
Рассмотрим вектор ![]()

Разложим старый базис по новому:
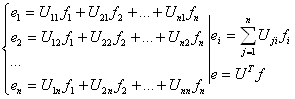
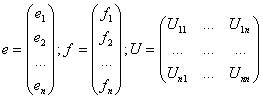
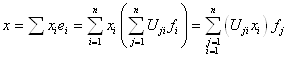
![]() ;
;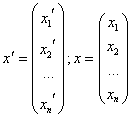
![]()
СБ - старый базис; СК - старые координаты.
НБ - новый базис; НК - новые координаты.
Итак: 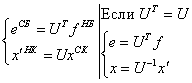
3) Системы линейных уравнений.
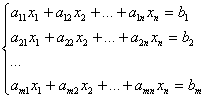 M уравнений, N неизвестных.
M уравнений, N неизвестных.

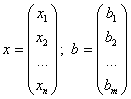
![]() - матричная форма записи систем уравнений.
- матричная форма записи систем уравнений.
![]() , I - фиксированный индекс.
, I - фиксированный индекс.
Классификация.
Если ![]() и
и ![]() , (то есть существует
, (то есть существует ![]() ), то это неоднородная система уравнений.
), то это неоднородная система уравнений.
Если ![]() , то есть
, то есть ![]() , то это однородная система уравнений.
, то это однородная система уравнений.
О решениях.
Если ![]() :
:
1) Имеет решения, то система уравнений называется совместной.
2) Не имеет решений, то система уравнений называется несовместной.
Совестная: 
| < Предыдущая | Следующая > |
|---|