Лекция №05. Подпространство и линейная оболочка. Операции над линейными пространствами. Изоморфизм линейных пространств. Базис и координаты

Рассмотрим L – линейное пространство.

-  Сколько в L линейно независимых векторов.

-  Какой из смысл.

Определение: Линейное пространство L называется N-мерным, а число N – размерностью, если в L существует N линейно независимых векторов, причём любые N+1 векторов линейно зависимы.

Определение: В N-мерном линейном пространстве L любая совокупность(система) N линейно независимых векторов называется базисом.

, - базисные векторы.

Определение: если - базис в , то для любого существуют числа : . Это разложение вектора по базису.

Теорема 8: В данном базисе координаты вектора определены однозначно

Доказательство(от противного): Пусть в базисе два набора чисел для вектора

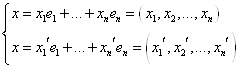
Так как линейно независимы, то все

Если в L существует любое число линейно независимых векторов, то L называется бесконечномерным линейным пространством.

Примеры базисов:

1)

2)

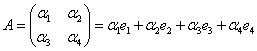
Базис Вейля

3)

.

4)

Подпространство и линейная оболочка

Пусть

L – множество

M – подмножество

Кроме того

L – линейное пространство

Тогда M – подпространство в L, если

Рассмотрим систему векторов .

Определение: Линейной оболочкой системы векторов называется множество всевозможных линейных комбинаций этих векторов. То есть: . Очевидно, что и является подпространством.

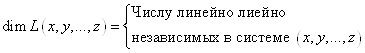
Пример: найти размерность и базис линейной оболочки , где

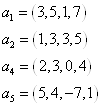
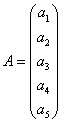
линейно независимы.

Операции над линейными пространствами.

- линейные пространства.

А)

Б)

А) Что такое .

Определение: линейное пространство L является прямой суммой и , если: выполняется одно из условий:

1)

2)

Теорема 9: Для того, чтобы , достаточно, чтобы

1)

2)

Тогда чтобы доказать, что, необходимо доказать, что - базис в L.

Рассмотрим:

Тогда .

Так как , то 0=0

< Предыдущая		Следующая >