Лекция №04. Линейное пространство. Примеры. Линейная зависимость. Базис и координаты. Размерность пространства. Примеры.

Определение 1: Ранг матрицы – это число её линейно независимых строк.

Рассмотрим минор порядка R:

Матрицы А .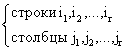

Определение 2: Рангом матрицы называется наивысший порядок минора матрицы, отличный от нуля.

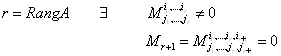
Теорема 5(о базисном миноре):

1. Тот минор , такой, что называется базисным. Строки и столбцы в базисном миноре называются базисными.

Теорема 5:

1) Базисные строки линейно независимы.

2) Любая строка матрицы является линейной комбинацией базисных строк.

Доказательство 1: Предположим, что базисные строки линейно зависимы, тогда по теореме 4 одна из строк является линейной комбинацией остальных. Но так как , а это базисный минор, то вычитая из данной строки эту линейную комбинацию, получаем нулевую строку, следовательно , следовательно базисные строки линейно независимы.

Доказательство 2:

Рассмотрим ;

Строка есть линейная комбинация базисных строк.

Свойства :

3) , если

Доказательство первого утверждения(свойства):

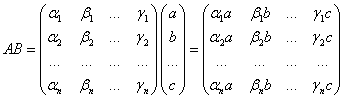
N строк линейно независимы

Так как в мы получаем N линейно независимых комбинаций строк , то очевидно, что число независимых строк возрастёт.

Доказательство 3-го утверждения(свойства):

Если , то из первого утверждения: , а из второго утверждения , значит

Элементарные преобразования:

1) Перестановка строк

2) Умножение строки на любое число, не равное нулю

3) Прибавление к элементам данной строки элементов других строк, умноженных на любое число.

Свойство: при элементарных преобразованиях ранг матрицы не меняется.

Теорема 6: Для того, чтобы , необходимо и достаточно, чтобы её строки были линейно независимы.

Доказательство (необходимость): Если , то строки линейно независимы. Так как , то среди строк имеется число линейно независимых строк, следовательно, совокупность всех строк является линейно независимой системой.

Доказательство (достаточность): Если строки линейно зависимы, то . Действительно, так как строки линейно зависимы, то одна из них есть линейная комбинация остальных. Тогда вычитая из этой строки данную линейную комбинацию, мы получаем нулевую строку, следовательно, .

Линейное пространство.

Рассмотрим множество L, произвольной природы.

Рассмотрим две операции элементов из L:

Определение: Множество называется линейным пространством, если в нём определены две операции – сложение и умножение и выполняется 8 аксиом(основных свойств):

Линейное пространство над полем вещественных, комплексных чисел определяет соответственно вещественное или комплексное линейное пространство.

Линейное пространство является также и группой.

Примеры:

1) - множество является линейный пространством при введении операций сложения и умножения.

R – группа относительно операции сложения.

- группа относительно операции умножения

3) - множество матриц порядка

4) - множество полиномов степени не выше, чем .

5) - множество функций, определённых и непрерывных на отрезке .

6) - нуль мерное пространство

Линейная зависимость

Пусть L – линейное пространство

- линейная комбинация векторов

- вектор есть линейная комбинация векторов.

Определение: система векторов называется линейно независимой, если их нулевая линейная комбинация выполняется только при . Если же среди существуют ненулевые элементы, то система линейно зависима.

Теорема 7: Для того, чтобы система была линейно зависимой, необходимо и достаточно, чтобы один из них линейно выражался через остальные(аналог теоремы 4).

< Предыдущая		Следующая >