Лекция №03. Линейная зависимость строк (теорема 4). Ранг и базисный минор. Теорема 5 о базисном миноре.

2) Теорема 6 о .

Свойства определителей:

3) Основное свойство

Рассмотрим:

Рассмотрим:

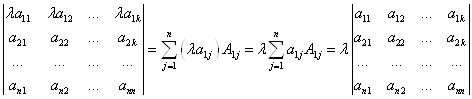
4) Линейное свойство.

Рассмотрим:

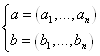
Пусть - линейная комбинация.

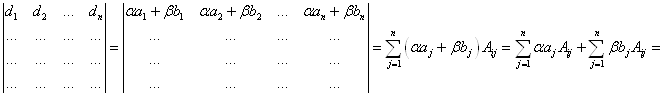
Величина определителя не меняется при следующих преобразованиях: если к элементам некоторой строки прибавить элементы другой строки, умноженной на любое число.

Теорема 2:

Рассмотрим две матрицы

- матрицы .

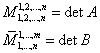
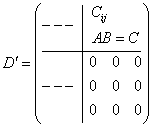
Обратная матрица.

Определение: матрица С называется правой обратной для матрицы А, если .

Матрица В называется левой обратной для матрицы А, если .

Докажем, что С=В.

Свойство:

Докажем:

Рассмотрим:

Теорема 3: Для того, чтобы у , необходимо и достаточно, чтобы

Доказательство(необходимость): Пусть 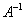существует, тогда.

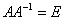Доказательство(достаточность): Пусть , тогда существует. Рассмотрим

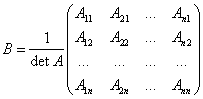. - алгебраическое дополнение элементов матрицы .

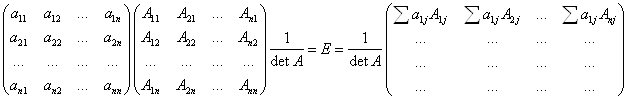
1) Рассмотрим строки:

- линейная комбинация строк ().

Определение: Строки называются линейно независимыми, если их нулевая линейная комбинация возможна только при , а если среди этих чисел есть одно не равное нулю, то строки называются линейно зависимыми.

Теорема 4: Для того, чтобы строки были линейно зависимыми, необходимо и достаточно, чтобы одна из строк линейно выражалась через другую.

Доказательство (необходимость):

Пусть линейно зависимы, тогда имеет место при .

Тогда

Доказательство(достаточность):

Пусть строка линейно выражается через остальные, тогда строки линейно зависимы. Следовательно,

Следовательно строки линейно зависимы.

< Предыдущая		Следующая >