Лекция №02. Группа. Группа подстановок. Определитель. Минор. Алгебраическое умножение.Теорема Лапласа. Свойства определителей. Обратная матрица. Матричные уравнения.

Преобразования:

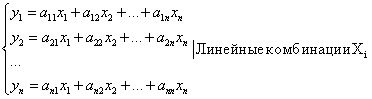
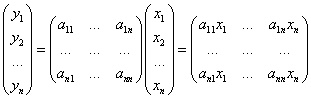
- матричная форма записи линейного преобразования.

Множество G называется группой, если в G задан закон композиции (операция), то есть задано правило, по которому двум элементам из G соответствует некоторый третий из G и выполняются аксиомы.

1) .

2) - ассоциативность.

3) е – единичный элемент.

4)

, тогда множество вещественных чисел есть группа, если композиция имеет вид .

- множество вещественных чисел за исключением нуля.

Группа подстановок.

Рассмотрим множество .

Определим операцию подстановки, то есть операцию перехода от одной перестановки к другой.

Из перестановки перешли к перестановке : . Определим произведение подстановки:

Чётность перестановки(и подстановки):

- чётная перестановка.

2) - множество матриц

- полностью антисимметричная N-линейная форма.

Первое определение:

N! перестановок и слагаемых.

- чётность перестановки.

.

Второе определение.

- минор с чертой (определитель матрицы А, у которой I строк и J столбцов).

- алгебраическое дополнение

ТЕОРЕМА ЛАПЛАСА(1749-1827)

Определим минор:

Минор с чертой: - определитель матрицы А, у которой вычеркнуты:

Минор без черты: - определитель из матрицы, составленной из элементов, стоящих на пересечении строк и столбцов

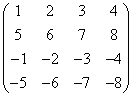
Теорема 1(Лапласа).

Для любых фиксированных строк имеет место формула:

Свойства определителей:

1)

2) Свойство антисимметрии:

< Предыдущая		Следующая >