Лекция №13. Свойства собственных значений и собственных векторов Эрмитова оператора. Унитарный оператор и его свойства. Билинейные и квадратичные формы. Классификация. Критерий Сильвестра. Ранг матрицы. Ранг квадратичной формы.

(1) Теорема 23: собственные векторы Эрмитова оператора ортогональны, а собственные значения вещественны.

Доказательство:

1)   Пусть - собственный вектор ;

Рассмотрим:

- вещественное число.

2)   - собственные векторы оператора Ф

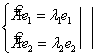Рассмотрим

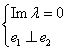
(2) - оператор

Определение: оператор называется унитарным, если выполняется условие:

Либо

Либо

Аналогично для матриц.

Если - унитарная матрица, то

Свойства унитарного оператора

1)   Унитарный оператор сохраняет скалярное произведение.

Рассмотрим 2 вектора и , тогда можно получить ещё два вектора: и .

- скалярное произведение

- скалярное произведение.

2)   Унитарный оператор сохраняет длины векторов.

В случае, когда - вещественна, имеем:

Если , то называется ортогональной.

Тогда

3)   Если ортогональны, то и и также ортогональны.

4)   Если - базис в .

- также базис.

для

5)   Собственные значения унитарного оператора по модулю равны 1.

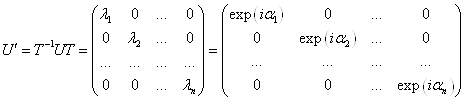
(3) Билинейные квадратичные формы.

Функция переменных

Определение:

- билинейная функция (форма), если - линейна по и по , то есть выполняется 4 условие.

Если (комплексные числа), то - полуторалинейная форма.

Общий вид билинейной формы:

- матрица билинейной формы

Пусть - симметрична

Рассмотрим случай, когда

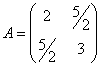
- квадратичная форма

- квадратичная форма

Классификация квадратичных форм:

1)   Если для всех , то квадратичная форма называется положительно определённой.

2)   Если для всех , то квадратичная форма называется отрицательно определённой.

3)   Если для всех , то квадратичная форма называется знаконеопределённой.

Критерий Сильвестра:

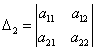
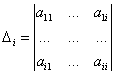
1)   Если все , то квадратичная форма положительно определена.

2)   Если все , то квадратичная форма отрицательно определена.

3)   Во всех других случаях квадратичная форма знаконеопределена.

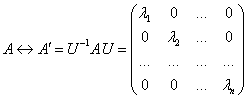
Виды квадратичных форм:

В различных базисах квадратичная форма имеет различный вид.

Матрица квадратичной формы преобразуется при переходе к другому базису по закону (вспомним, что ).

1)   - общий вид.

2)   - канонический вид.

3)   - нормальный вид.

Сигнатура (знак):

- сигнатура.

Евклидово пространство:

Трёхмерное пространство:

Пространство Минковского (четырёхмерное): , , , .

< Предыдущая