6. Приложение 1

Некоторые линии, встречающиеся в аналитической геометрии.

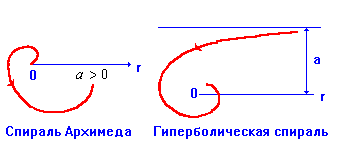
1) Спираль Архимеда:

2) Гиперболическая спираль:

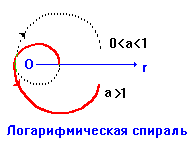
3) Логарифмическая спираль:

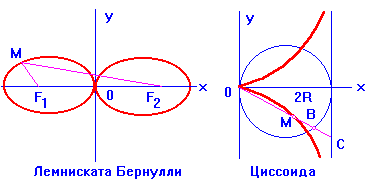
4) Лемниската Бернулли:

.

Характерное свойство линии:

Где

5) Циссоида:

Характерное свойство: для всякого луча

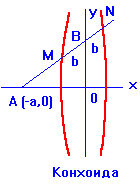
6) Конхоида: ;

Характерное свойство: для всякого луча

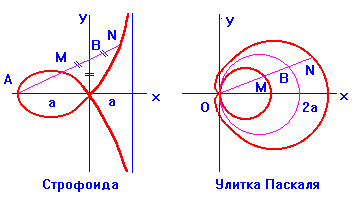
7) Строфоида ;

Характерное свойство: для всякого луча

8) Улитка Паскаля

;

Характерное свойство: для всякого луча

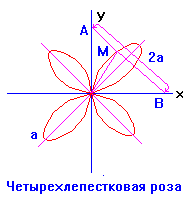
9) Четырехлепестковая роза

;

Характерное свойство: всякая точка М этой кривой есть основание перпендикуляра, опущенного из начала координат на отрезок постоянной длины , движущегося так, что концы его все время находятся на координатных осях.

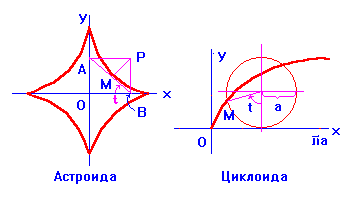
10) Астроида

;

Характерное свойство: всякая точка М этой кривой есть основание перпендикуляра к отрезку , постоянной длины А, движущемуся так, что концы его все время находятся на координатных осях.

11) Циклоида ;

Характерное свойство: кривая совпадает с траекторией точки М окружности радиуса А, которая катится без скольжения по оси Ох (в начальный момент точка М она находилась в начале координат).

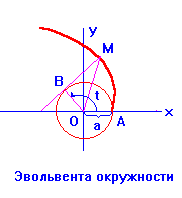
12) Эвольвента (развертка) окружности

;

Характерное свойство: каждая точка М этой кривой есть конец нити, которая, оставаясь натянутой, разматывается с окружности (в начальный момент конец нити находится в точке ).

13) Эпициклоида

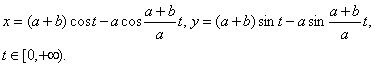
Характерное свойство: кривая совпадает с траекторией точки М окружности радиуса A, которая катится без скольжения по окружности (в начальный момент точка М находится в положении ); в частном случае, кривая называется Кардиоидой:

14) Гипоциклоида

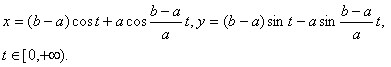
Характерное свойство: кривая совпадает с траекторией точки М окружности радиуса A, которая катится без скольжения по окружности , оставаясь внутри ее (в начальный момент точка М находится в положении ); в частном случае, кривая является Астроидой.

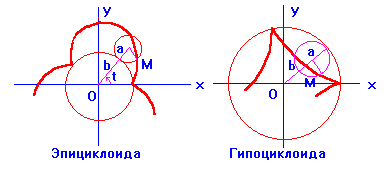
15) Полукубическая парабола ;

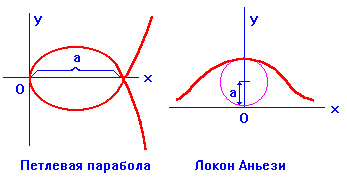
16) Петлевая парабола ;

17) Локон Аньези ;

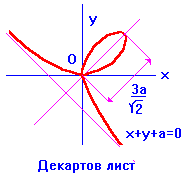
18) Декартов лист .

< Предыдущая		Следующая >