7. Приложение 2

Некоторые поверхности второго порядка, встречающиеся в аналитической геометрии

1. Эллипсоид.

Уравнение эЛлипсоида .

Величины называются Полуосями эллипсоида. Если они различны между собой, то эллипсоид называется Трехосным. Предположим , тогда эллипсоид образуется вращением эллипса вокруг оси . Если эллипсоид образован вращением эллипса вокруг его большой оси, то он называется Вытянутым, вокруг меньшей оси - Сжатым.

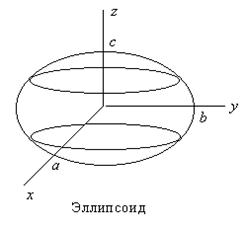
Для построения поверхности используется «метод параллельных сечений». Перепишем исходное уравнение в виде

.

Изменяя в пределах от до , в сечении получаем эллипсы с полуосями и 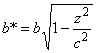. Как видно, при (плоскость ) имеем эллипс , а при - точку . Между этими предельными значениями , по мере увеличения от нуля до , в сечении имеем набор эллипсов, полуоси которых непрерывно уменьшаются от значений и до нуля.

2. Гиперболоиды.

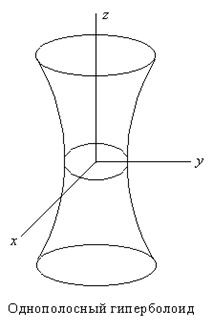
1) Однополосный гиперболоид .

Величины называются Полуосями гиперболоида. Если, например, , тогда гиперболоид образуется вращением гиперболы вокруг оси .

Для построения поверхности используется «метод параллельных сечений». Перепишем исходное уравнение в виде

.

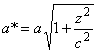Изменяя в пределах от до , в сечении получаем эллипсы с полуосями и .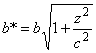

Однополосный гиперболоид относится к, так называемым, Линейчатым Поверхностям, т. е. полностью состоящих из прямых. Чтобы это увидеть, следует записать исходное уравнение в виде

.

Как видно, уравнение состоит из произведений линейных множителей, т. е. прямых.

2) Двухполосный гиперболоид .

Величины называются Полуосями гиперболоида. Если, например, , тогда гиперболоид образуется вращением гиперболы вокруг оси .

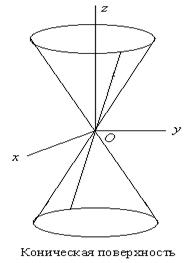
3. Конус.

Уравнение конической поверхности, или просто конуса, имеет вид

.

Заметим, что уравнение однородное и имеет степень однородности равную двум. При имеем , следовательно конус проходит через начало координат. В § 24 показано, что коническая поверхность состоит из бесконечного числа прямых (называемых Образующими конуса), проходящих через начало координат (Вершину конуса). В сечениях, параллельных плоскости , имеем эллипсы с полуосями и .

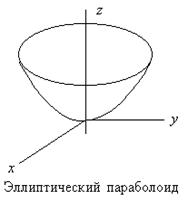
4. Параболоиды.

1) Эллиптический параболоид .

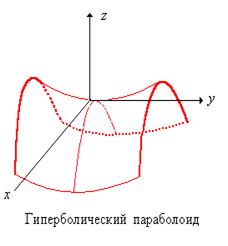
2) Гиперболический параболоид .

4. Цилиндрические поверхности.

Уравнения цилиндрических поверхностей не содержат переменной , поэтому их разновидности получаются из, рассмотренных ранее, кривых второго порядка в плоскости неограниченным параллельным продолжением плоской линии вдоль положительной и отрицательной направлений оси .

1) Эллиптический цилиндр: ; в частности, при - круговой цилиндр .

2) Гиперболический цилиндр: .

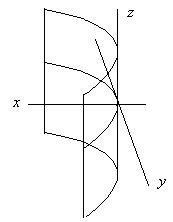
3) Параболический цилиндр: .

В качестве примера приведем только поверхность парабо-лического цилиндра.

< Предыдущая