5.3. Цилиндрические и конические поверхности

Определение 1. Поверхность называется Цилиндрической с образующей параллельной оси , если для любой точки этой поверхности, прямая, проходящая через нее и параллельная оси , целиком лежит на поверхности .

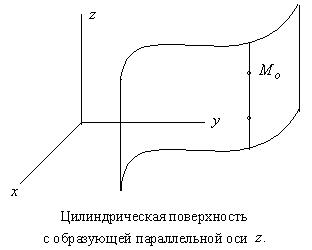
Аналогично определяются цилиндрические поверхности с образующими параллельными осям и соответственно.

Теорема 1. Всякое уравнение вида (связывающее переменные и , и не содержащее ) определяет цилиндрическую поверхность с образующей параллельной оси .

Доказательство. Пусть точка лежит на поверхности , определяемой уравнением , т. е. и задана прямая, параллельная оси и проходящая через эту точку. Абсцисса и ордината этой прямой соответственно равны , а аппликата имеет произвольное значение. В уравнение не входит , а . Поэтому рассматриваемая прямая является образующей цилиндрической поверхности .

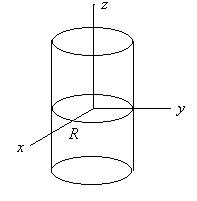
Пример 1. Круглый цилиндр радиуса R с центром в начале координат и образующими параллельными оси :

Определение 2. Поверхность называется Конической с вершиной в начале координат, если для любой точки этой поверхности, прямая, проходящая через эту точку и начало координат, целиком лежит на поверхности .

Теорема 2. Уравнение в котором является однородной функцией порядка M (т. е. для любого числа имеем ), определяет коническую поверхность.

Доказательство. Пусть точка лежит на поверхности , определяемой уравнением , т. е. и задана прямая, проходящая через начало координат О и эту точку. Если М есть произвольная точка прямой, то векторы и коллинеарные и тогда найдется такое число , что . Следовательно, для однородной функции имеем

.

В силу равенства имеем .

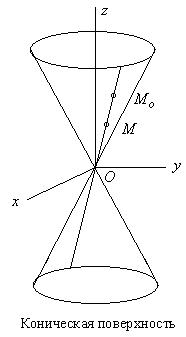
Пример 2. Уравнение круглого конуса . Функция является однородной функцией второго порядка.

< Предыдущая		Следующая >