5.1. Уравнения линий и поверхностей в пространстве. Уравнение линий и поверхностей в декартовой системе координат

Определение 1. Геометрическое место точек пространства, коор-динаты которых в заданной декартовой системе удовлетворяют уравнению

, (1)

Называется Поверхностью в этой системе координат.

Примеры:

1. есть уравнение сфе-ры радиуса с центром в точке .

В частности, если центр сферы в начале координат, то и уравнение имеет вид .

2. есть уравнение плоскости.

3. есть уравнение единственной точки (0,0,0).

4. Уравнение не определяет никакой геометрический образ, т. к. .

Определение 2. Поверхность называется Алгебраической, если функция в уравнении (1) является алгебраическим полиномом (т. е. является суммой конечного числа слагаемых вида ).

Алгебраическая поверхность называется поверхностью порядка , если функция является полиномом -й степени. Например, общее уравнение второй степени

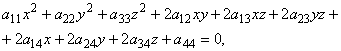
Где - заданные действительные числа, определяет некоторую поверхность второго порядка. Примеры таких поверхностей приведены в ПРИЛОЖЕНИИ 2.

Замечание. Аналогично, как в случае плоской кривой, вводится понятие распадающейся алгебраической поверхности S На две поверхности и , если .

Линию в пространстве можно рассматривать как пересечение двух поверхностей и , т. е. линия определяется системой двух уравнений

(2)

5. Система

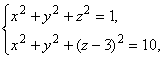
Определяет в плоскости окружность единичного радиуса с центром в начале координат. В самом деле, при уравнения системы совпадают с уравнением .

< Предыдущая		Следующая >