4.3. Исследование уравнения второго порядка

Рассмотрим общее уравнение кривых второго порядка

. (1)

1-й случай : .

С помощью поворота осей координат и параллельного переноса уравнение (1) может быть приведено к виду

. (2)

1) Если коэффициенты имеют одинаковые знаки, то имеется три возможности:

А) Знак противоположен знаку . Перенесем в правую часть и разделим на этот коэффициент. Уравнение примет вид:

Где Это Каноническое уравне-ние эллипса.

Б) Знак совпадает со знаком . По аналогии со случаем а) получим:

Это уравнение Мнимого Эллипса.

В) = 0. Уравнение примет вид:

Реально это уравнение Единственной точки , Но, часто уравнение называют Парой мнимых пересекающихся прямых, т. к.

,

Где - мнимая единица, .

2) Если коэффициенты имеют разные знаки, то имеется две возможности:

А) Знак противоположен знаку . Перенесем в правую часть и разделим на этот коэффициент. Уравнение примет вид:

Где Это уравнение Гиперболы.

Б) Уравнение примет вид:

Прямые и пересекаются в начале координат. Это уравнение пары пересекающихся прямых.

2-й случай : например, .

С помощью поворота осей координат и параллельного переноса уравнение (1) может быть приведено к виду

. (3)

А) Группируем члены следующим образом:

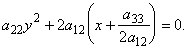
Сделаем параллельный перенос вдоль оси : . Уравнение примет вид:

Это уравнение параболы.

Б) Уравнение примет вид: Если знак противоположен знаку , то

Это уравнение пары параллельных прямых.

Если знак совпадает со знаком , то

Это Пара мнимых параллельных прямых.

Если , то имеем уравнение

Это Пара совпадающих прямых.

Теорема. Пусть в декартовой системе координат задано уравнение второго порядка

.

Тогда существует такая декартова система, в которой это уравнение принимает один из следующих девяти канонических видов:

< Предыдущая		Следующая >