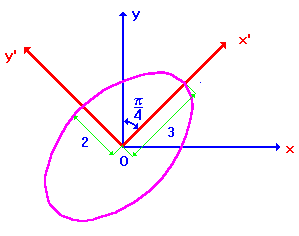
4.2*. Кривые второго порядка при повороте осей координат

Исходим из уравнения

(1)

И покажем, что всегда можно выбрать угол поворота координатных осей так, что "смешанный" член обратится в нуль. Пусть система координат X"O'y" получена поворотом системы X'O'y' вокруг начала O' на угол .

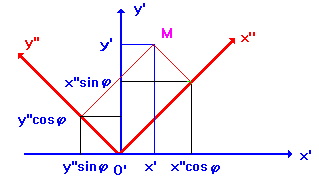
Как видно из рисунка, "старые" и "новые" координаты связаны равенствами

(2)

Подставим их в уравнение (1)

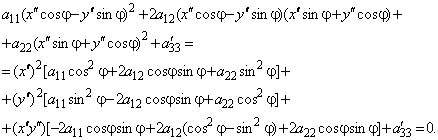Последнюю квадратную скобку перепишем в виде и выберем угол j так, чтобы она обращалась в нуль:

.

Разделим это уравнение на , получим . Откуда найдем искомый угол

. (3)

Обозначая в (2) первые квадратные скобки , а вторые , получим уравнение (20.4) в "новой" системе координат

. (4)

ВЫВОД: Для кривой, заданной уравнением (1), поворотом осей координат можно "уничтожить" смешанный (билинейный) член и преобразовать его к уравнению (4); при этом свободный член не изменяется.

Пример 1. Поворотом осей координат установить тип кривой, заданной уравнением

.

Сравнивая с уравнением (20.4), находим

.

По формуле (3) найдем угол поворота .

Итак, для приведения кривой к каноническому виду следует сделать поворот осей на угол , при этом формулы перехода даются (2):

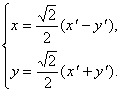
Подставим эти значения в исходное уравнение, получим

.

Разделим уравнение на свободный член и перенесем его в правую часть уравнения, получим - это эллипс с полуосями .

< Предыдущая		Следующая >