3.5. Полярные уравнения кривых второго порядка
Рассмотрим произвольную кривую ![]() второго порядка и поместим начало полярной системы в фокус этой кривой.
второго порядка и поместим начало полярной системы в фокус этой кривой.

По определению кривых второго порядка ![]() . Как видно из рисунка,
. Как видно из рисунка, ![]() , а
, а ![]() . Отсюда получим уравнение
. Отсюда получим уравнение
![]() (1)
(1)
Это полярное уравнение эллипса при ![]() , правой ветви гиперболы при
, правой ветви гиперболы при ![]() и параболы при
и параболы при ![]() .
.
Замечание 1. Для левой ветви гиперболы ![]()
![]() ,
, ![]() .
.
(легко проверяется при ![]() имеем
имеем ![]() ) имеем уравнение
) имеем уравнение ![]()
Замечание 2. Полярное уравнение окружности не следует из (1), а выводится из уравнения ![]() с использованием формул перехода к полярным координатам
с использованием формул перехода к полярным координатам
![]()
.
Пример 1. Написать уравнение прямой ![]() в поляр-ных координатах.
в поляр-ных координатах.
Решение. Перепишем уравнение прямой в нормированном виде
![]()
![]()
![]()
![]()
Перейдем к полярным координатам: ![]() , и учтем, что
, и учтем, что ![]() :
:
![]()
![]()
Уравнение прямой в полярных координатах можно получить иначе. Сделаем рисунок.
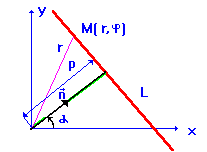
Откуда видно:
![]()
Пример 2. Записать уравнения заданных кривых:
А) в полярных координатах: б) в декартовых координатах:
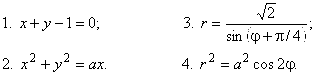
![]() Перейдем к полярным координатам
Перейдем к полярным координатам ![]()
![]() Тогда,
Тогда,
![]()
![]()
![]()
Перейдем к декартовым координатам
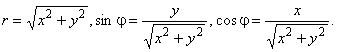
Тогда,
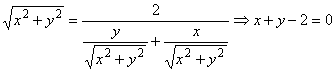 - прямая.
- прямая.
![]()
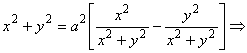
![]() - лемниската Бернулли.
- лемниската Бернулли.
| < Предыдущая | Следующая > |
|---|