3.3. Каноническое уравнение гиперболы
Определение. Гиперболой называется геометрическое место точек плоскости для которых абсолютная величина разности расстояний до фокусов ![]() и
и ![]() есть величина постоянная, т. е.
есть величина постоянная, т. е.
![]() .
.
В координатах это выражение имеет вид
![]() .
.
После стандартного метода "уничтожения" радикалов (возведения обеих частей уравнения в квадрат (см. пример 1. §14.)) получим каноническое уравнение гиперболы
![]() (1)
(1)
Где ![]() .
.

Свойства гиперболы:
1. Гипербола имеет две взаимно перпендикулярные оси симметрии ![]() и
и ![]() (главные оси гиперболы) и центр симметрии О (центр гиперболы).
(главные оси гиперболы) и центр симметрии О (центр гиперболы).
Утверждение следует из того, что замена координат![]() на
на ![]() или
или ![]() или
или ![]() не изменяет вид уравнения (1).
не изменяет вид уравнения (1).
2. Гипербола имеет две асимптоты, определяемые уравнения-ми
![]() . (2)
. (2)
В самом деле, из уравнения (1) имеем 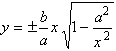 .
.
Выберем, например, первую кривую (со знаком "+") и найдем разность ординат прямой ![]() и гиперболы
и гиперболы ![]() в точке
в точке ![]() :
:
![]() .
.
Заметим теперь, что ![]() при
при ![]() .
.
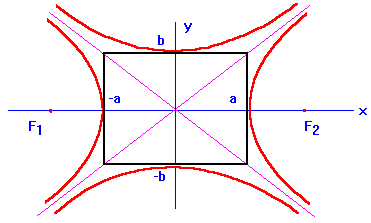
Замечание. Первых двух свойств достаточно для построения гиперболы: построим так называемый Характеристический Прямоугольник гиперболы размерами ![]() и
и ![]() , проводим асимптоты
, проводим асимптоты ![]() и, наконец, ветви гиперболы.
и, наконец, ветви гиперболы.
3. Гипербола имеет так называемую сопряженную по отношению к ней гиперболу, уравнение которой следует из определения ![]() или
или
![]() . (3)
. (3)
4. Эксцентриситет гиперболы ![]() определяется выражением
определяется выражением 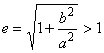 , которое следует из связи
, которое следует из связи ![]() . Обратим внимание на то, что эксцентриситет гиперболы больше единицы в отличии от эллипса, для которого он заключен между нулем и единицей.
. Обратим внимание на то, что эксцентриситет гиперболы больше единицы в отличии от эллипса, для которого он заключен между нулем и единицей.
5. Для директрис гиперболы
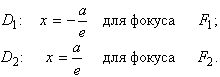
Имеет место аналогичное как для эллипса свойство:
![]() ,
,![]() .
.
Поскольку для гиперболы ![]() , то ее директрисы расположены в пределах характеристического прямоугольник по оси
, то ее директрисы расположены в пределах характеристического прямоугольник по оси ![]() и пред-ставляют собой пару прямых, параллельных оси
и пред-ставляют собой пару прямых, параллельных оси ![]()
Пример 1. Найти точки гиперболы ![]() , находящиеся на расстоянии 7 до фокуса
, находящиеся на расстоянии 7 до фокуса ![]() .
.
Решение. Найдем координаты фокуса ![]() :
:
![]()
Согласно условию задачи ![]() . Выразим
. Выразим ![]() из уравнения гиперболы
из уравнения гиперболы 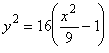 , подставим в данное уравнение и приведем подобные члены, получим квадратное уравнение
, подставим в данное уравнение и приведем подобные члены, получим квадратное уравнение

Его корни ![]()
![]() - лишний корень, т. к.
- лишний корень, т. к. ![]() . Тогда
. Тогда ![]() Отв.
Отв. ![]()
Пример 2. Найти фокальные радиусы точки ![]() гиперболы
гиперболы ![]() и ее расстояния до директрис.
и ее расстояния до директрис.
Решение. Фокальные радиусы ![]() . Эксцен-триситет гиперболы
. Эксцен-триситет гиперболы
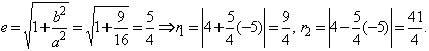
Расстояния до директрис:
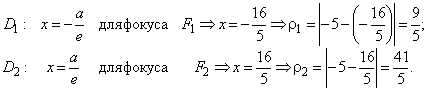
| < Предыдущая | Следующая > |
|---|