3.2. Эксцентриситет и директрисы эллипса

Определение 1. Эксцентриситетом эллипса называется величи-на .

Используя связь , выразим и подставим его в определение, найдем еще одно выражение для эксцентриситета

. (1)

Откуда сразу следует, что . Кроме того, заметим, что при имеем окружность, а при - отрезок прямой . Таким образом, геометрически эксцентриситет эллипса характеризует меру его "вытянутости". С увеличением эксцентриситета эллипс все более "вытягивается", вырождаясь в отрезок прямой при .

Определение 2. Директрисами и эллипса называются прямые

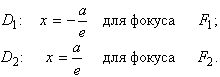
Поскольку , то директрисы эллипса расположены за пределами эллипса и представляют собой пару прямых, параллельных оси

Теорема. Отношение расстояния от любой точки М эллипса до фокуса к расстоянию от этой же точки М до директрисы равно эксцентриситету : .

Доказательство. Построим рисунок.

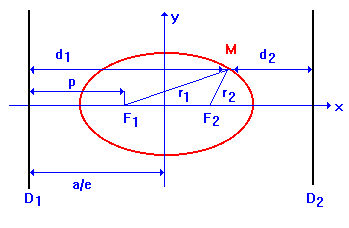
Для фокуса имеем:

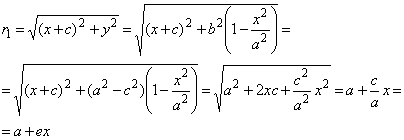
и . Откуда следует . Аналогично, для фокуса

Следствие. Выражения для расстояний от фокусов эллипса до произвольной точки М этого эллипса

.

< Предыдущая		Следующая >